Предмет: Алгебра,
автор: mitrofanovatana52
пожалуйста докажите тождество
Приложения:
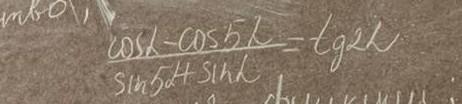
Ответы
Автор ответа:
1
Ответ:
Доказано!
Объяснение:
Докажите тождество cosα - cos5α/sin5α + sinα = tg2α
Ч.Т.Д
Применил следущие формулы:
Похожие вопросы
Предмет: Українська мова,
автор: katerinapedorenko00
Предмет: Алгебра,
автор: onsovicnina
Предмет: Экономика,
автор: vitaoleynik86
Предмет: Музыка,
автор: Cyxapuk98
Предмет: Алгебра,
автор: ketrinkryt