Question

Помогите пожалуйста решить задачу

Answer 1

Ответ:

1

Пошаговое объяснение:

Дано:

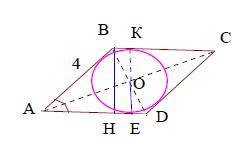
ABCD - ромб

АВ=ВС=CD=AD=4

∠A =30°

r = ОЕ -  ? (r - радиус вписанной окружности)

____________

1) Центр ромба - это точка пересечения его диагоналей, которая является цетром вписанной окружности.

Чтобы найти расстояние от центра до стороны, нужно опустить ⊥ из центра на сторону:

ОЕ ⊥ AD, OE = r .

Продложим ОЕ до ВС → КЕ ⊥ ВС

2) построим высоту ромба ВН:

ВН ⊥AD

ΔАВН - прямоугольный и ∠А = 30°

В прямоугольном Δ-ке против угла в 30° лежит катет, равный половине гипотенузы:

ВН = АВ/2 = 2

3) Т.к. ВН⊥AD , ВН ⊥ВС и КЕ⊥AD, KE⊥BC, то ВН = КЕ = 2.

Т.к. О- центр ромба или центр вписанной окружности, то

КО = ОЕ = r =  2/2 =1