Предмет: Математика,
автор: kostya66747tty
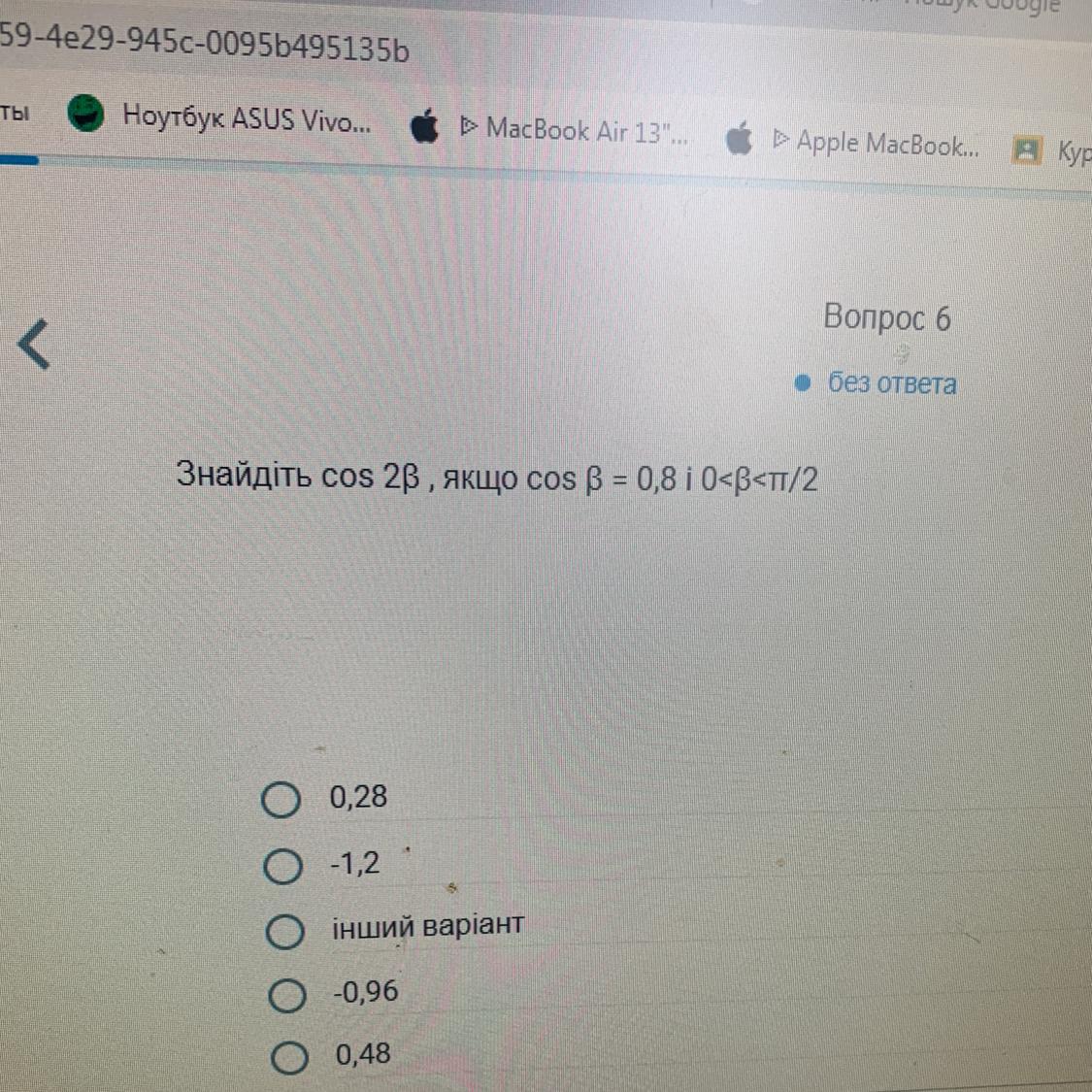
Знайдіть cos 2B, якщо соs B = 0,8 i 0
Приложения:
Ответы
Автор ответа:
2
Ответ:
0,28
Пошаговое объяснение:
Знайдіть cos2β , якщо cosβ = 0,8 i 0<β<π/2
Согласно формуле косинуса двойного аргумента :
Чтобы найти sinβ - воспользуемся тригонометрическим тождеством sin²β+cos²β = 1 :
По условию угол принажлежит 1-ой четверти , синус угла в первой четверти положительный , поэтому
Теперь найдём косинус двойного аргумента :
Похожие вопросы
Предмет: Қазақ тiлi,
автор: olgarybokoneko
Предмет: Українська мова,
автор: arina0384arina
Предмет: Алгебра,
автор: Аноним
Предмет: Английский язык,
автор: alex22025
Предмет: Математика,
автор: pakulewa198314