Предмет: Геометрия,
автор: bezobmejen2121
СРОЧНО 4 ПРОШУ ВАС
ГЕОМЕТРИЯ 9 класс
Приложения:
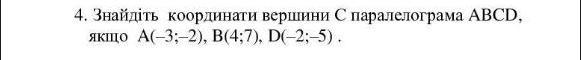
Ответы
Автор ответа:
1
Ответ:
С(5;4)
Объяснение:
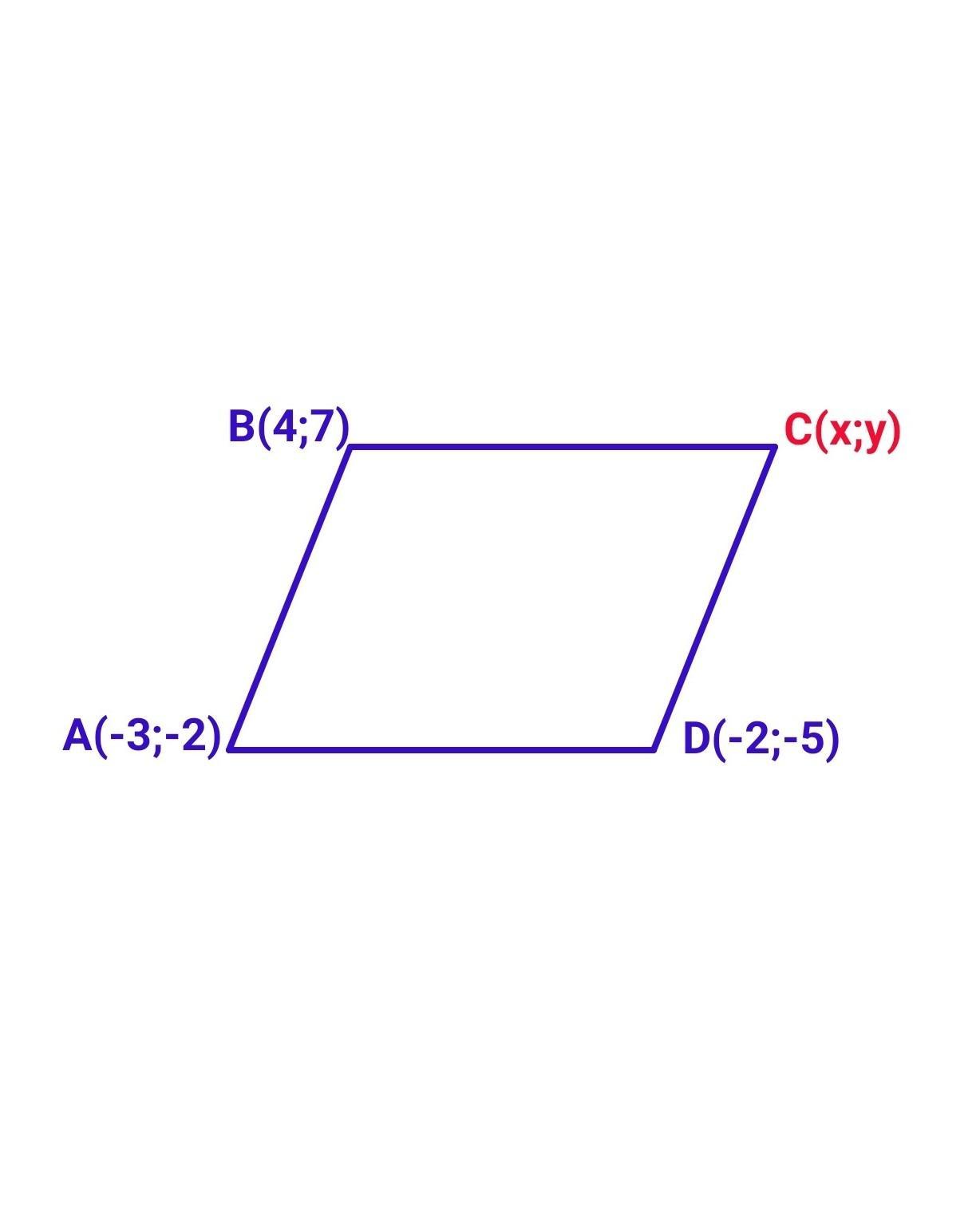
Знайдіть координати вершини С паралелограма ABCD, якщо А(-3;-2), В(4;7), D(-2;-5).
Якщо ABCD - паралелограм, то у нього протилежні сторони попарно паралельні та рівні: AD=BC.
Але тоді й вектори є рівними, а отже є рівними і відповідні координати цих векторів.
Нехай точка С має координати С(х;у).
- Для знаходження координат вектора треба від координат кінця вектора відняти відповідні координати початку
Тоді вектори мають координати:
Отже:
Рівні вектори мають рівні відповідні координати, тому:
х-4=1, у-7=-3.
Звідси:
х=5, у=4.
Тоді точка С має координати С (5;4).
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: vikachichi666
Предмет: Физика,
автор: abc348976
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: olimolimov18