Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить задачу,
Приложения:

Ответы
Автор ответа:
1
Ответ:
Задан степенной ряд .
Применяем признак Даламбера к ряду, составленному из абсолютных величин членов исходного ряда :
Проверяем сходимость ряда в граничных точках .
Этот ряд расходится, так как не выполняется необходимый признак
сходимости : .
Это тоже расходящийся знакочередующийся ряд, не выполняется
первое условие признака Лейбница : .
Область сходимости заданного ряда:
Автор ответа:
0
Объяснение:
надеюсь помогла, ответ уверена что правильный.
Приложения:

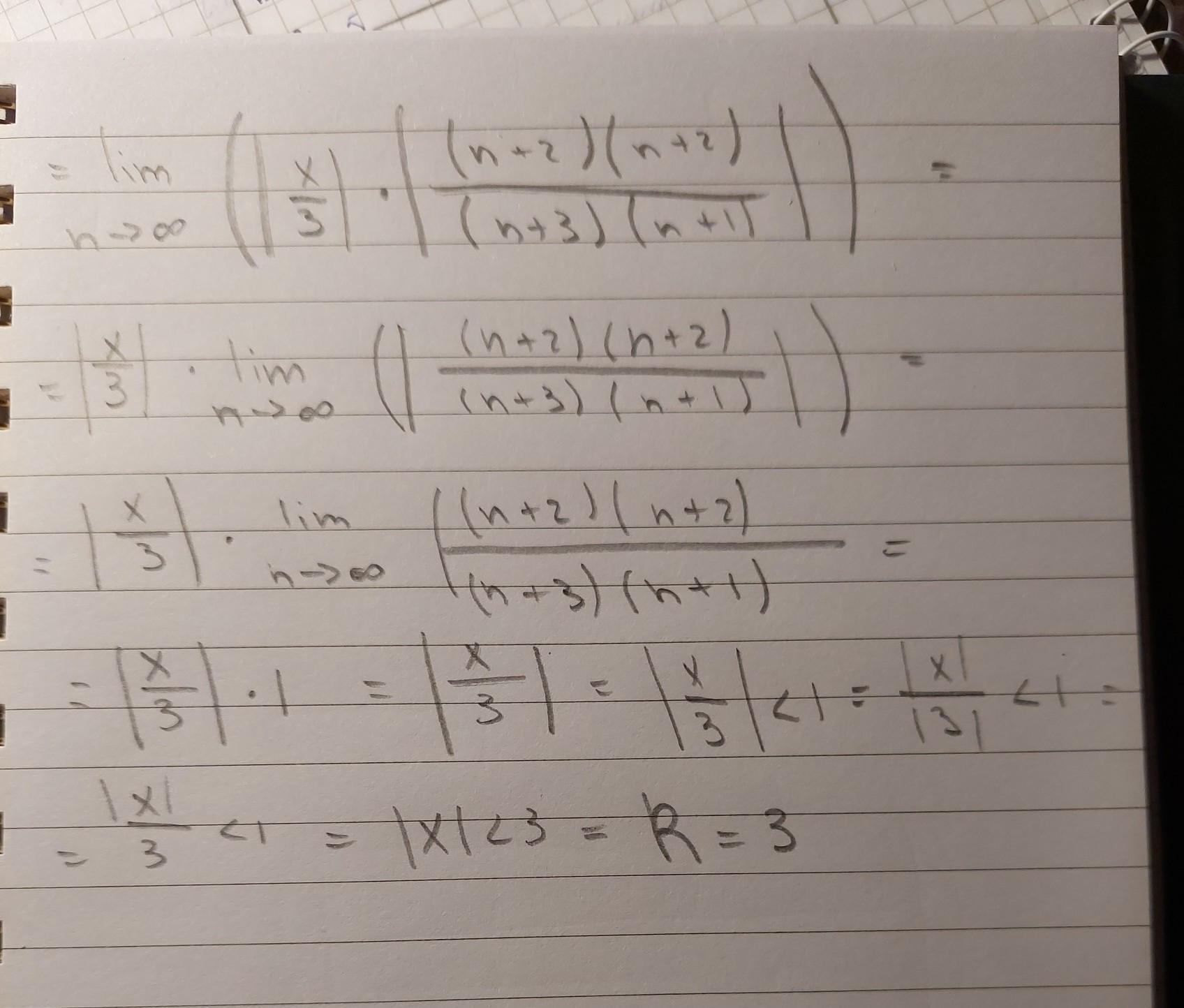
Похожие вопросы
Предмет: Литература,
автор: zabelinadasa269
Предмет: Українська література,
автор: stepurana
Предмет: Математика,
автор: kadochnikovaekaterin
Предмет: Литература,
автор: Аноним
Предмет: Геометрия,
автор: kitmotion12367