Предмет: Алгебра,
автор: milanasmadic
Допоможіть будь-ласка якомога швидше
Приложения:
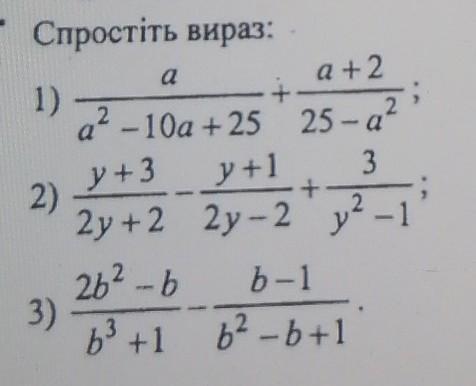
Ответы
Автор ответа:
0
1)
2)
3)
Похожие вопросы
Предмет: Другие предметы,
автор: galinakajdas91
Предмет: Математика,
автор: egornovikov815
Предмет: Українська література,
автор: susyoyoylyly
Предмет: Литература,
автор: mariyam200690
Предмет: Астрономия,
автор: madmarvn23