Предмет: Алгебра,
автор: kamilmatematik100504
решите только 10 .................
Приложения:
siestarjoki:
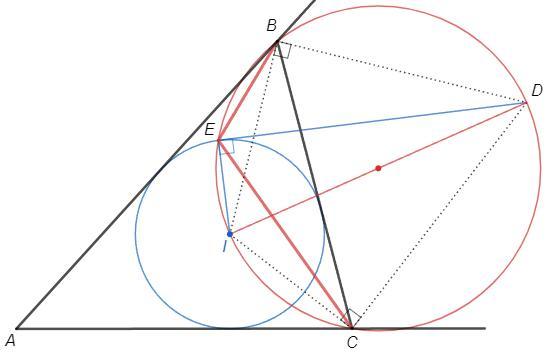
I - инцентр. BICD на одной окружности, ID - диаметр (биссектрисы внешнего и внутреннего углов перпендикулярны). IED - прямой => точка E на этой окружности. Тогда BEC=BIC=90+A/2=111
Ответы
Автор ответа:
1
I - центр вписанной окружности ABC, точка пересечения биссектрис.
Биссектрисы внешнего и внутреннего углов треугольника перпендикулярны (т.к. это биссектрисы смежных углов)
Отрезок ID виден из точек B и C под прямым углом - точки B-I-C-D лежат на окружности диаметром ID.
Радиус, проведенный в точку касания, перепендикулярен касательной.
Отрезок ID виден из точки E под прямым углом - точка E также лежит на окружности диаметром ID.
Тогда ∠BEC=∠BIC (вписанные углы, опирающиеся на одну дугу)
∠BIC =90° +∠A/2 (угол между биссектрисами внутренних углов треугольника)
(A+B+C=180° ; из треугольника BIC: ∠BIC +B/2 +C/2=180° => BIC =90°+A/2)
∠BEC =90° +42°/2 =111°
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: 380988823030
Предмет: Информатика,
автор: ilia2w2
Предмет: Геометрия,
автор: marasykdenis
Предмет: Музыка,
автор: olyachka2107