Question

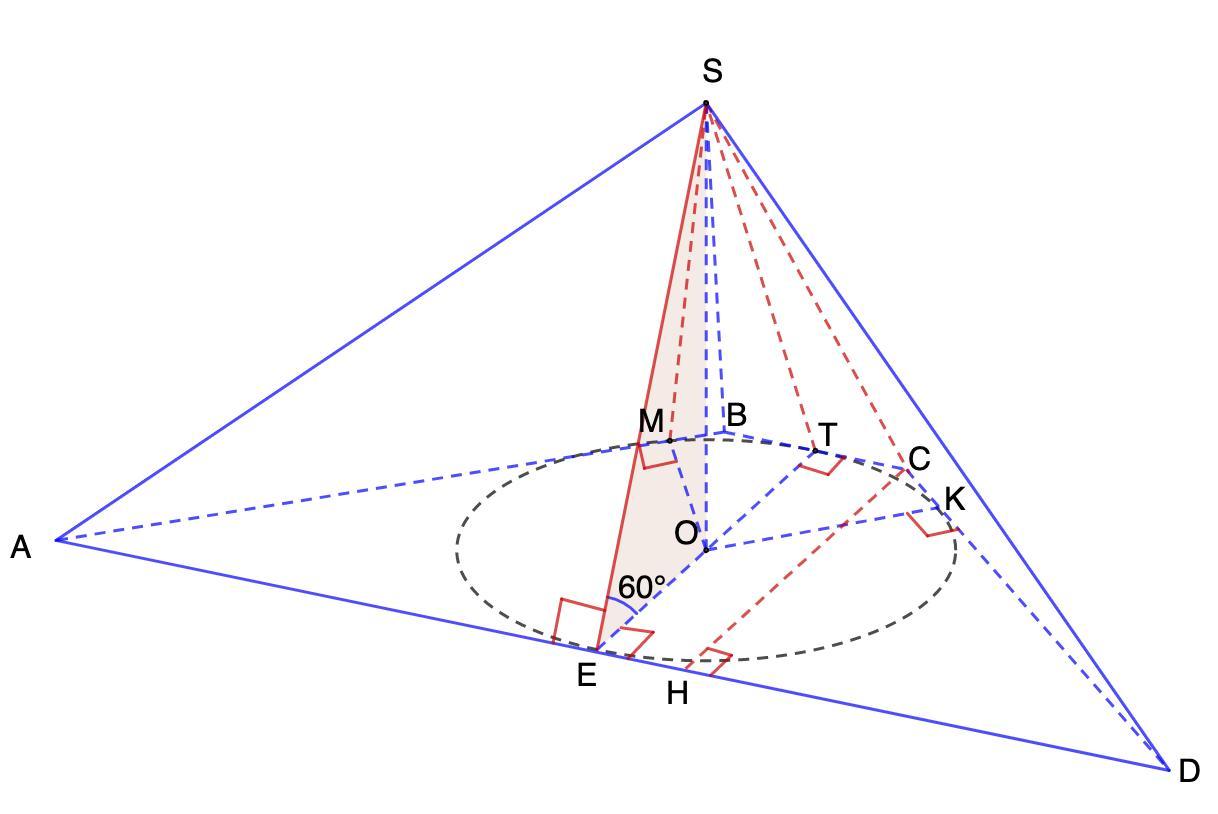
В основі піраміди лежить рівнобічна трапеція, основи якої дорівнюють 3 см і 27 см. Усі двогранні кути при основі дорівнюють 60°. Знайдіть площу повної поверхні цієї піраміди.

В основе пирамиды лежит равносторонняя трапеция, основания которой равны 3 см и 27 см. Все двугранные углы при основании равны 60°. Найдите площадь полной поверхности этой пирамиды.

Answer 1

Ответ:

Площадь полной поверхности этой пирамиды равна 405 см².

Объяснение:

В основании пирамиды лежит равнобедренная трапеция, основания которой равны 3 см и 27 см. Все двугранные углы при основании равны 60°. Найдите площадь полной поверхности этой пирамиды.

Дано: SABCD - пирамида;

ABCD - равнобедренная трапеция;

ВС = 3 см; AD = 27 см.

Все двугранные углы при основании равны 60°.

Найти: Sполн.

Решение:

Двугранный угол - угол наклона боковой грани к основанию.

• Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.

⇒ ОМ, ОТ, ОК; ОЕ - радиусы вписанной окружности.

• Радиус, проведенный в точку касания перпендикулярен касательной.

⇒ ОМ ⊥ AB, ОТ ⊥ BC, ОК ⊥ CD; ОЕ ⊥ AD.

• Прямая, проведённая в плоскости через основание наклонной, перпендикулярная к её проекции на эту плоскость, перпендикулярна и самой наклонной.

⇒ SМ ⊥ AB, SТ ⊥ BC, SК ⊥ CD; SЕ ⊥ AD.

∠SMO =∠STO = ∠SKO = ∠SEO = 60° - линейные углы, которыми измеряются двугранные углы.

• Площадь поверхности пирамиды складывается из площади основания и площадей боковых граней.

1. Найдем площадь основания.

• Если в четырехугольник вписана окружность, то суммы противоположных сторон равны.

⇒ BC + AD = AB + CD = 3 + 27 = 30 (см)

AB = CD = 15 (см)

Проведем высоту СН.

• Высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на части, меньшая из которых равна полуразности оснований.

⇒ $\displaystyle HD=\frac{AD-BC}{2} =\frac{27-3}{2}=12\;_{(CM)}$

По теореме Пифагора найдем высоту СН:

$\displaystyle CH=\sqrt{CD^2-HD^2}=\sqrt{225-144}=9\;_{(CM)}$

$\displaystyle S_{OCH}=\frac{BC+AD}{2} \cdot{CH}=\frac{3+27}{2}\cdot9=135\;_{(CM^2)}$

2. Найдем апофему.

Рассмотрим ΔESO - прямоугольный.

ОЕ = СН : 2 = 4,5 см

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ЕSO = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ ЕS = ОЕ · 2 = 9 (см)

• Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.

3. Найдем площади боковых граней.

Площадь треугольника равна половине произведения основания на высоту.

$\displaystyle S(ASD)=\frac{1}{2}AD\cdot{ES}=\frac{1}{2}\cdot27\cdot9 =\frac{243}{2}=121,5 \;_{(CM^2)}$

$\displaystyle S(BSC)=\frac{1}{2}BC\cdot{TS}=\frac{1}{2}\cdot3\cdot9 =\frac{27}{2} =13,5\;_{(CM^2)}$

$\displaystyle S(ASB)=S(CSD)=\frac{1}{2}AB\cdot{MS}=\frac{1}{2}\cdot15\cdot9 =\frac{135}{2} =67,5\;_{(CM^2)}$

Площадь полной поверхности равна:

Sполн = 135 + 121,5 +13,5 + 67,5 + 67,5 = 405 (см²)

Площадь полной поверхности этой пирамиды равна 405 см².

#SPJ1