Question

У правильній трикутній піраміді через сторону основи проведено площину, перпендикулярно до протилежного бічного ребра. Визначити площу утвореного перерізу, якщо сторона основи дорівнює 1 см, а висота піраміди - 4 см.

Answer 1

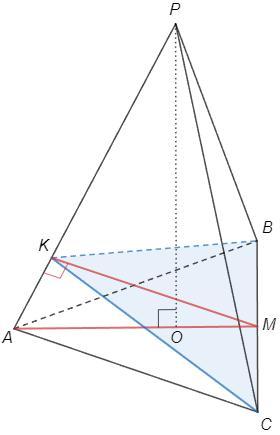
Из вершин B и C основания проведем перпендикуляры к ребру PA.

Правильная пирамида, боковые грани - равные треугольники.

Перпендикуляры, как соответствующие отрезки, пересекут ребро PA в одной точке K.

BK⊥PA, CK⊥PA => (BKC)⊥PA

Сечение является проекцией основания ABC на плоскость BKC.

M - середина BC, AM и KM - высоты/медианы основания и сечения.

∠AMK - угол между плоскостями основания и сечения

∠AMK =90°-∠KAM =∠APO

Правильная пирамида, вершина P падает в центр описанной окружности основания.

AO =R =AC/2sin60° =1/√3

PA =√(AO^2+PO^2) =√(1/3 +16) =7/√3

cosAPO =PO/PA =4√3/7 =cosAMK

S(BKC) =S(ABC) cosAMK =v3/4 *4√3/7 =3/7