Предмет: Математика,
автор: danabana
допоможіть знайти! даю 20 балів!!!
Приложения:
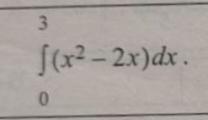
Ответы
Автор ответа:
0
Ответ:
Ответ:
Пошаговое объяснение:
Вычислить интеграл:
Для решения надо знать:
А также формулу Ньютона - Лейбница:
Вычислим:
Ответ:
Похожие вопросы
Предмет: География,
автор: vikavoronja
Предмет: Математика,
автор: dinisbilous399
Предмет: Математика,
автор: isden0832
Предмет: Английский язык,
автор: magma19821981