помогите пожалуйста

Ответы
Объяснение:
Объяснение:Решить систему неравенств:
х²+у² < 49
ху ≤ 5
====================================
РЕШЕНИЕ:
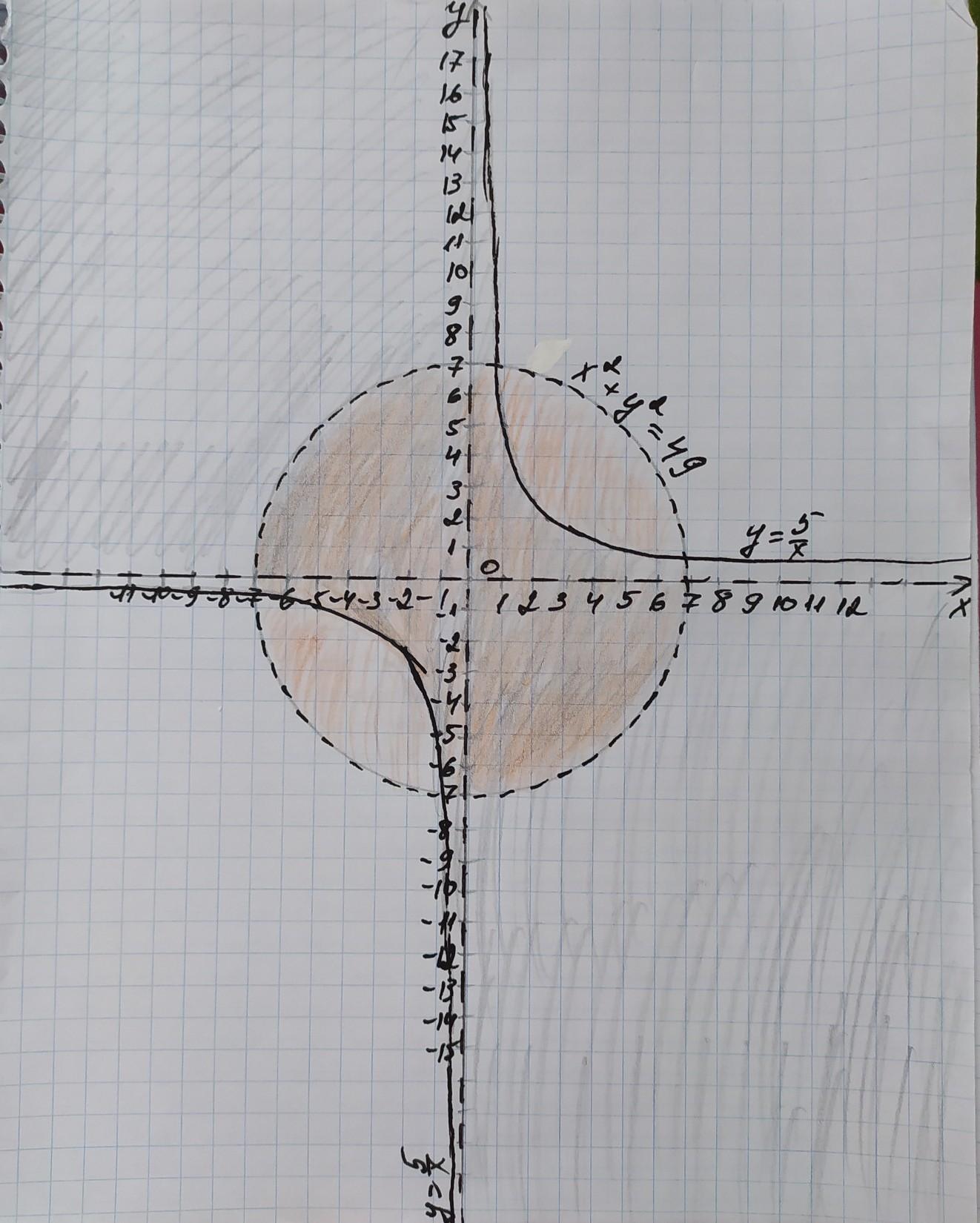
Записав неравенство х²+у² < 49 в виде формулы графика: х²+у²=49, то получим уравнение окружности с центром в начале координат и радиусом 7, так как √49=7. Со второго неравенства ху ≤ 5, выразим у и так же представим в виде уравнения:у ≤ 5/х; у=5/х, начертим оба этих графика.Точки построения графика у=5/х, х≠0.х=1 →у=5; х=2 →у=2,5; х=2,5 →у=2; х=5 →у=1х= –1 →у= –5; х= –2 →у= –2,5; х= –2,5 →у= –2;х= –5 →у= –1.
После построения, нам нужно определить области, которые, согласно неравенству будут входить в решение. Так как в неравенстве
х²+у² < 49, то заштриховываем область внутри круга, (оранжевым цветом) при этом точки окружности обозначаем пунктиром, так как они не входят в решение, потому что знак равенства строгий.Теперь определимся с неравенством ху ≤ 5.Определимся с верхней веткой. Возьмём любую координату, например (1; 5) – х= 1, у=5. Но по условию неравенства у ≤ 5, тогда заштриховываем ту область, которая находится под веткой, в том числе и 4-ю четверть, при этом поскольку х≠0, то оси координат мы обозначаем пунктиром, так как они не входят в решение. Определимся со нижней веткой в 3-ей четверти.Также возьмём любую координату, например(–1; –5). По условию неравенства
ху ≤ 5
–у ≤ 5
у ≥ –5
значит заштриховываем область, которая находится над дугой и закрашиваем всю область между дугами серым цветом в том числе за пределами круга в 3–й четверти. Область заштрихованная серым и оранжевым цветами вместе области будут являться решением этой сиситемы.