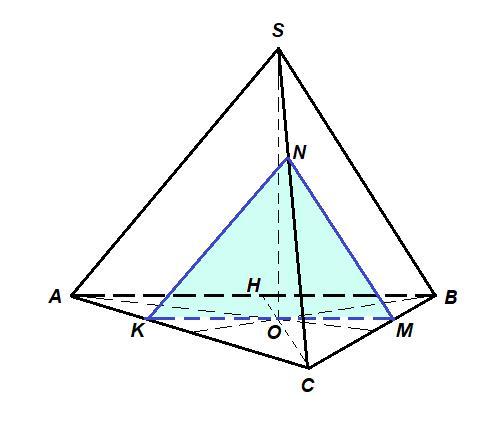
Ребро правильного тетраедра SABC дорівнює 6. Знайдіть площу перерізу тетраедра площиною, яка проходить через центр грані АВС паралельно грані ABS.
Ответы
Ответ:
4√3 см²
Объяснение:
В правильном тетраэдре все ребра равны.
АВС - правильный треугольник.
Центр грани АВС - точка пересечения медиан треугольника АВС, точка О.
В плоскости АВС через точку О проводим прямую, параллельную АВ.
Она пересечет ребра АС и ВС в точках К и М соответственно.
В плоскости ACS проводим прямую, параллельную AS. Она пересечет ребро SC в точке N.
Соединяем точки N и М.
Признак параллельности плоскостей:
- если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.
Так как КМ║АВ и KN║AS, то KMN║ABS.
KMN - искомое сечение.
- Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
Поэтому ΔCKM ~ ΔCAB.
По свойству медиан:
⇒
Так как СО и СН - медианы, проведенные к сходственным сторонам, то
Аналогично, ΔCKN ~ ΔCAS (КN║AS),
Тогда ΔCMN ~ ΔCBS по двум пропорциональным сторонам и равному углу между ними:
,
- ∠C - общий.
Тогда
Доказали, что
,
значит ΔKMN ~ ΔABS по трем пропорциональным сторонам.
см
По формуле площади правильного треугольника:
см²