Question

Даю 25 балів, якщо можна то розписати на листочку

Знайти більшу основи рівнобічної трапеції, діагональ якої перпендикулярна до бічної сторони і утворює з більшою основою кут у 30° .
А менша основа дорівнює 30 см​

Answer 1

Ответ:

60 см

Объяснение:

Дано:

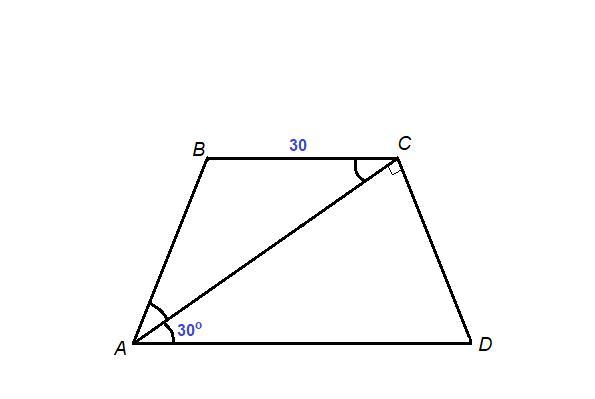
ABCD - трапеция, АВ = CD, ВС = 30 см,

АС⊥CD, ∠CAD = 30°.

Найти: AD.

Решение:

• Сумма острых углов прямоугольного треугольника равна 90°.

ΔACD: ∠ACD = 90°,

 ∠CDA = 90° - ∠CAD = 90° - 30° = 60°

∠BAD = ∠CDA = 60° как углы при основании равнобедренной трапеции.

∠ВАС = ∠BAD - ∠CAD = 60° - 30° = 30°

∠BCA = ∠CAD = 30° как внутренние накрест лежащие при пересечении AD║ВС секущей АС.

Итак, в треугольнике АВС ∠ВАС = ∠ВСА, значит треугольник равнобедренный,

АВ = ВС = 30 см

CD = AB = 30 см

ΔACD: ∠ACD = 90°, против угла в 30° лежит катет, равный половине гипотенузы. Гипотенуза - AD.

AD = 2CD = 2 · 30 = 60 см