Question

РЕШИТЕ ПОЖАЛУЙСТА УМОЛЯЯЯЮ ,С ОБЪЯСНЕНИЕМ АААААААААААААААА

Answer 1

Ответ:

$\left\{\begin{array}{l}x^2+y\leq 3\\x+2y > -2\end{array}\right$  

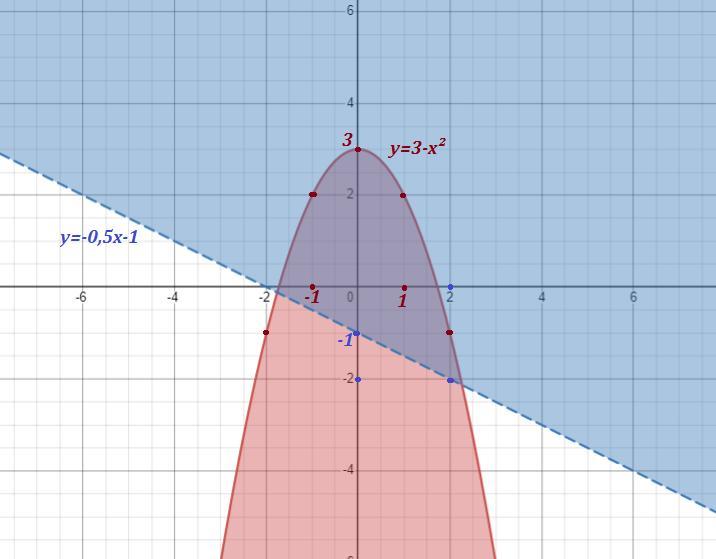
$x^2+y\leq 3\ \ \Rightarrow \ \ \ y\leq 3-x^2$  - это часть плоскости, расположенная внутри параболы  $y=3-x^2$  . Ветви параболы направлены вниз, вершина в точке (0;3) . Сама парабола входит в область . Область закрашена красным цветом .

$x+2y > -2\ \ \Rightarrow \ \ 2y > -x-2\ ,\ y > -0,5x-1$  - это часть плоскости, расположенная выше прямой  у=-0,5х-1  (полуплоскость) , причём сама прямая в область не входит, поэтому нарисована пунктирной линией . Прямая проходит через точки (0;-1) и (2;-2) .  Полуплоскость закрашена синим цветом .

Искомая область - часть плоскости, лежащая внутри параболы , но выше прямой , сама прямая в область не входит .