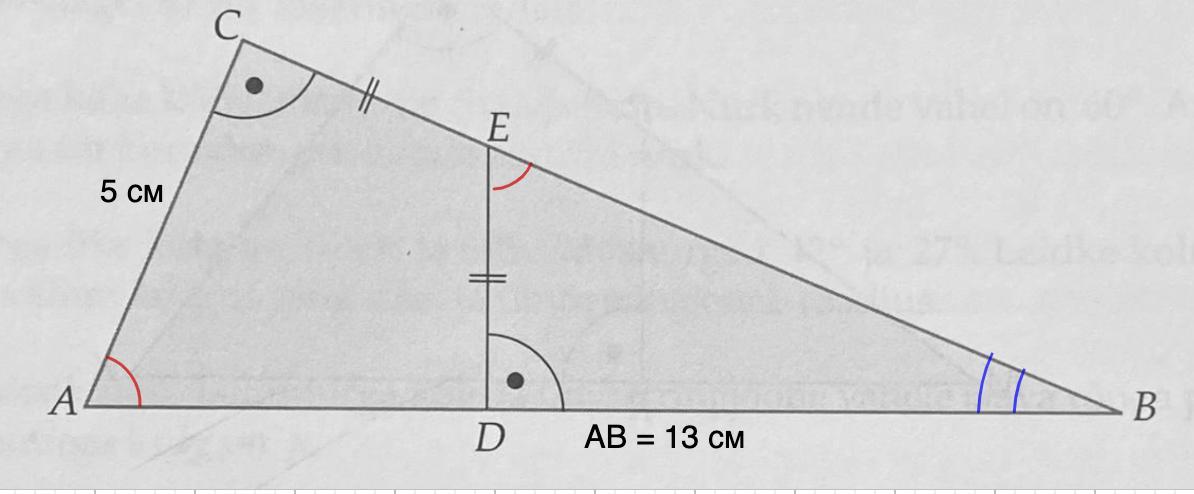
Дан прямоугольный треугольник ABC, известно что CE=ED, AB=13cm и AC=50мм.
1) Найдите длину отрезка CE.
2) Вычислите длину описанной окружности треугольникаABC.
3) Вычислите площадь вписанной окружности треугольникаABC.
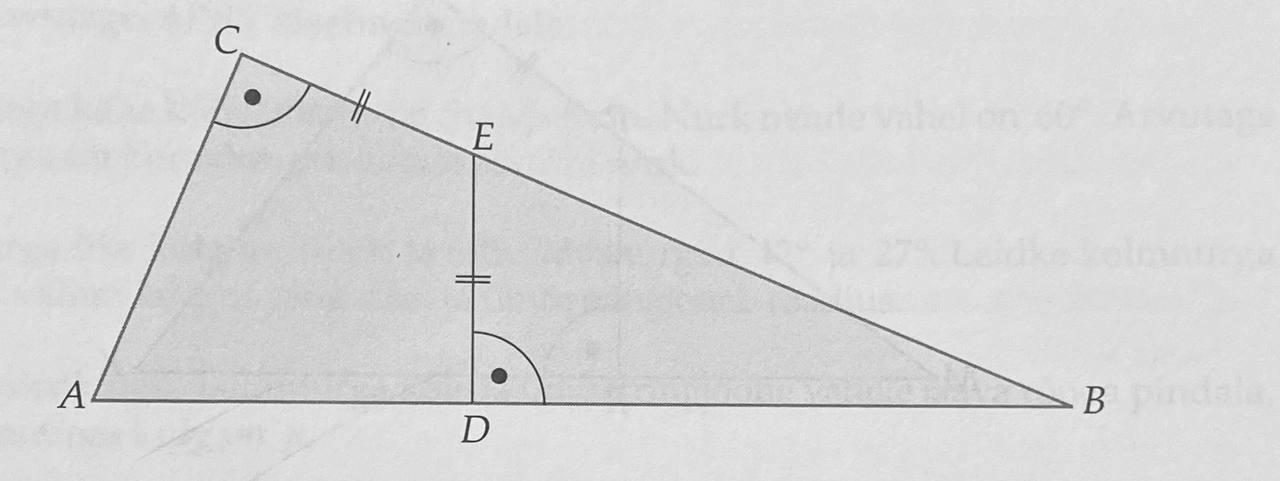
Ответы
Ответ:
1) Длина отрезка СЕ равна см.
2) Длина описанной окружности около треугольника ABC равна 13π см.
3) Площадь вписанной окружности треугольника ABC равна 4π см².
Объяснение:
Дан прямоугольный треугольник ABC, известно что CE=ED, AB=13 см и AC=50 мм.
1) Найдите длину отрезка CE.
2) Вычислите длину описанной окружности треугольника ABC.
3) Вычислите площадь вписанной окружности треугольника ABC.
Дано: ΔАВС - прямоугольный;
CE = ED;
АВ = 13 см; АС = 50 мм = 5 см.
Найти: 1) СЕ; 2) L - длину описанной окружности; 3) S вписанной окружности.
Решение:
1) Найдите длину отрезка CE.
1. Рассмотрим ΔАВС - прямоугольный.
По теореме Пифагора найдем СВ:
СВ² = АВ² - АС² = 169 - 25 = 144 ⇒ СВ = √144 = 12 (см)
2. Рассмотрим ΔDEB и ΔАВС - прямоугольные.
∠В - общий.
⇒ ΔDEB ~ ΔАВС (по двум углам)
Пусть СЕ = ED = х см; тогда ЕВ = (12 - х) см.
Запишем отношения сходственных сторон:
Длина отрезка СЕ равна см.
2) Вычислите длину описанной окружности треугольника ABC.
Найдем радиус описанной окружности.
- Центр описанной окружности лежит на середине гипотенузы.
⇒ R = AB : 2 = 13 : 2 = 6,5 (см)
- Длина окружности равна L = 2πR.
⇒ L = 2π · 6,5 = 13π (см)
Длина описанной окружности около треугольника ABC равна 13π см.
3) Вычислите площадь вписанной окружности треугольника ABC.
- Найдем радиус вписанной окружности в прямоугольный треугольник по формуле:
, где a и b - катеты, с - гипотенуза.
- Площадь круга найдем по формуле: S = πr²
S = π · 2² = 4π (см²)
Площадь вписанной окружности треугольника ABC равна 4π см².