Question

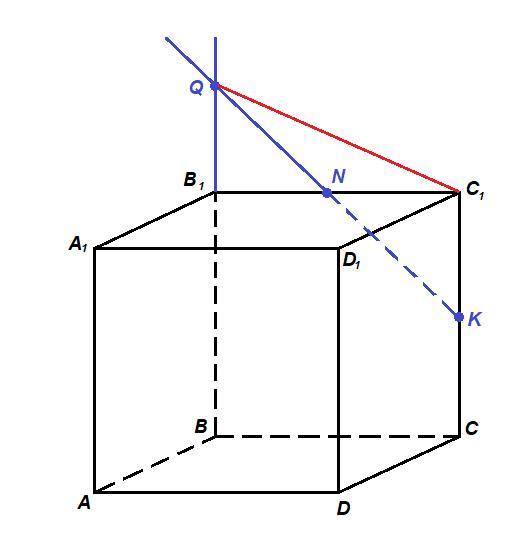
Точки N и K — середины ребер B1C1 и CC1 куба ABCDA1B1C1D1, ребро которого 8. Прямая NK пересекает плоскость AA1B1 в точке Q. Найдите длину отрезка QC1

Помогите пожалуйста, срочно.

Answer 1

Ответ:

4√5

Объяснение:

Построим точку пересечения прямой NK с плоскостью АА₁В₁:

• - прямая NK лежит в плоскости В₁С₁С;
• - плоскость  В₁С₁С пересекает плоскость АА₁В₁ по прямой ВВ₁;
• - находим точку пересечения прямой NK с прямой ВВ₁, это точка Q.

ΔQB₁N = ΔKC₁N по катету и прилежащему острому углу:

• В₁N = C₁N, так как N середина В₁С₁,
• ∠QNB₁ = ∠KNC₁ как вертикальные,
• ∠QB₁N = ∠KC₁N = 90°.

Из равенства треугольников следует, что

QB₁ = KC₁ = 0,5 CC₁ = 0,5 · 8 = 4

Из прямоугольного треугольника QB₁C₁ по теореме Пифагора:

QC₁ = √(QB₁² + B₁C₁²) = √(4² + 8²) = √(16 + 64) = √80 = 4√5