Предмет: Геометрия,
автор: Bananabond
У правильній трикутній піраміді кут між апофемами дорів нює 60°. Знайдіть площу повної поверхнi ради, якщо сторона Її основи дорівнює 4 см.
Ответы
Автор ответа:
0
Ответ:
12 + 4√3 см²
Объяснение:
Пирамида правильная, значит в основании лежит правильный треугольник.
Площадь основания:
см²
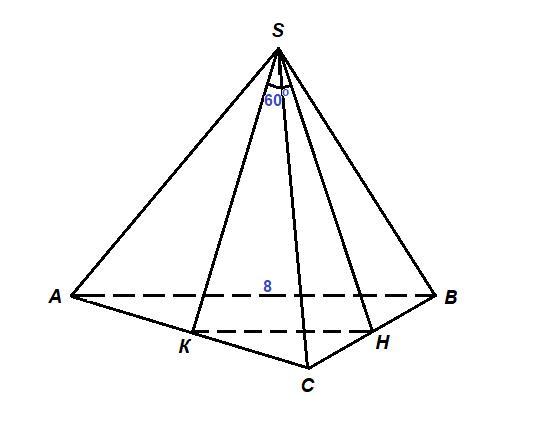
К и Н - середины ребер АС и ВС.
КН = 0,5 АВ = 0,5 · 4 = 2 см как средняя линия треугольника АВС.
SK = SH - апофемы.
∠KSH = 60° - угол между апофемами.
ΔKSH равнобедренный с углом 60°, значит он равносторонний.
SK = KH = 2 см
- Площадь боковой поверхности правильной пирамиды можно найти как половину произведения периметра основания на апофему:
Sбок. = 0,5 Росн. · SK = 0,5 · (4 · 3) · 2 = 12 см²
Площадь полной поверхности:
S = Sбок. + Sосн.
S = 12 + 4√3 см²
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: rogovenkofedor
Предмет: Физика,
автор: zivotovtimur11
Предмет: Физика,
автор: zorenkoivan4
Предмет: Окружающий мир,
автор: Аноним