Предмет: Математика,
автор: elizabeth9493
На чертеже показаны три больших окружности с одинаковым радиусом и четыре меньших окружностей одинакового радиуса. Центры всех окружностей и точки касания лежать на одной прямой. Радиус маленьких окружностей равны 1. Чему равна закрашенная площадь?
пожалуйста
Приложения:
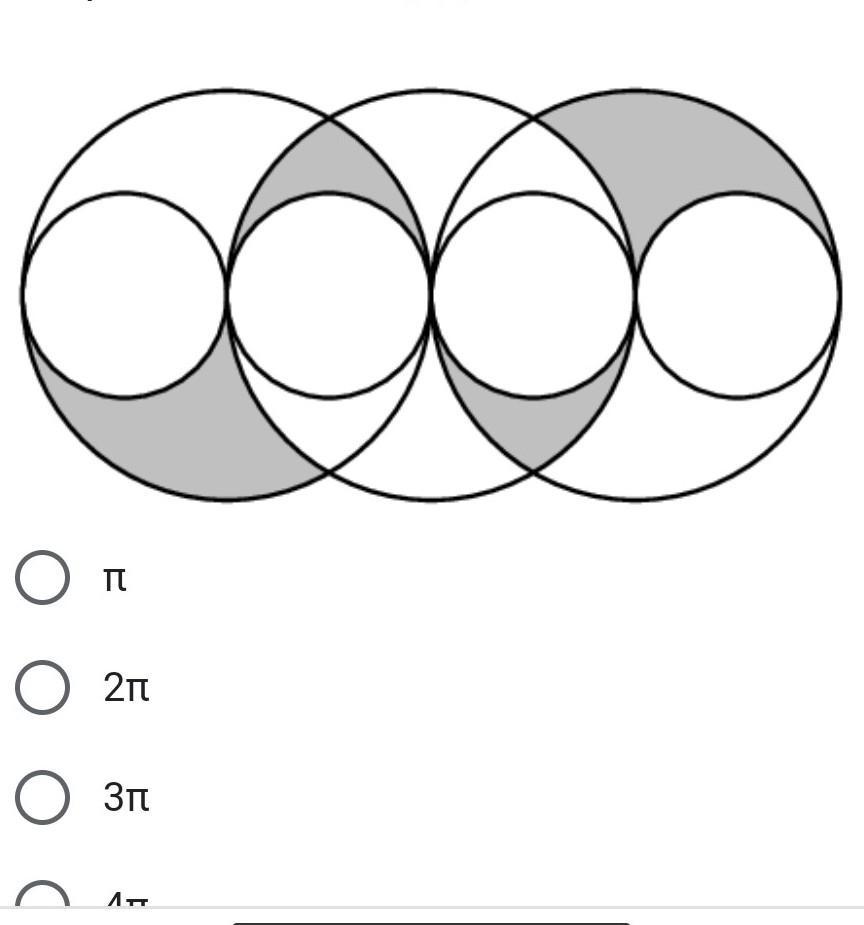
Ответы
Автор ответа:
3
Ответ:
2π
Пошаговое объяснение:
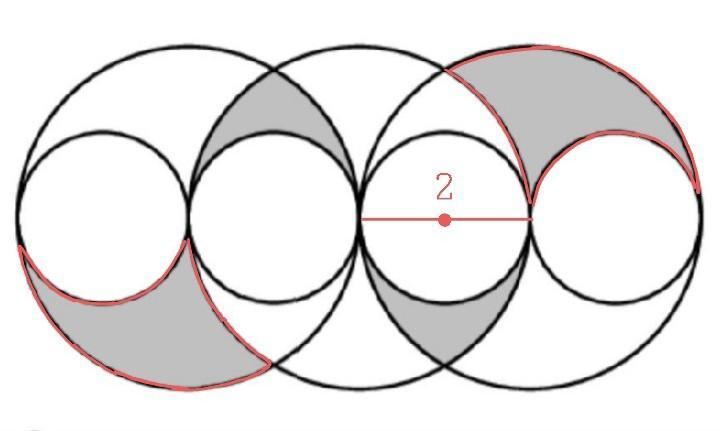
Обратим внимание , выделенные красным цветом закрашенные части(см.рис.) совпадают с незакрашенными частями по середине расположенной большой окружности (не считая две маленькие вписанные в неё окружности) , тогда можно считать ,что окружность, расположенная по середине полностью закрашенна , не учитывая маленьких окружностей , вписанных в неё , чтобы найти площадь закрашенной части , нужно из площади большой окружности отнять площадь маленьких окружностей.
- Найдем площадь маленьких окружностей , радиус маленьких окружностей равна 1 (по условию) .
Площадь находится по формуле:
- Тогда S мал.окр. = π·1² = π , значит , каждый из двух маленьких окружностей с площадью равной π
- Радиус большой окружности будет равна сумме радиусов вписанных окружностей , тогда радиус большой окружности будет равен 2-ум . S бол.окр. = π·2² = 4π
- S зак.части = 4π-π-π = 2π
Приложения:
Похожие вопросы
Предмет: Химия,
автор: piatnichuki93
Предмет: Английский язык,
автор: ahoroshko19
Предмет: Математика,
автор: kotovaa23
Предмет: Английский язык,
автор: marinastegina
Предмет: Другие предметы,
автор: tomaveer09