Предмет: Математика,
автор: korrawki
100 баллов. довести тотожність з фото
Приложения:
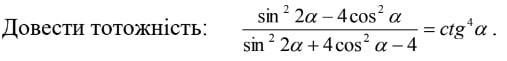
Ответы
Автор ответа:
3
Основное тригонометрическое тождество:
Формула синуса двойного угла:
Преобразуем:
Похожие вопросы
Предмет: Литература,
автор: s083938591az
Предмет: Английский язык,
автор: islamhashiev012
Предмет: Астрономия,
автор: fatimakerimbekova5
Предмет: Математика,
автор: Аноним