Предмет: Алгебра,
автор: venem5rv
постройте график тригонометрической функции y=1/1+ctg²x определите а) нули функции; б) асимптоты функции
Ответы
Автор ответа:
2
Ответ:
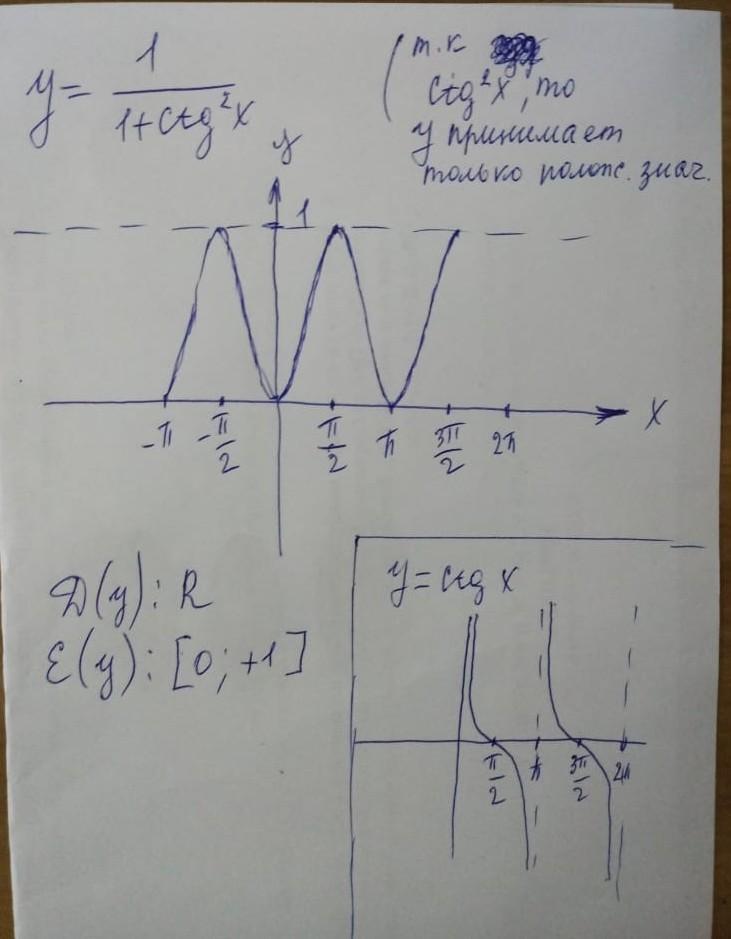
Подробное решение на фото.
Объяснение:
Удачи!
Приложения:
Автор ответа:
0
Ответ:
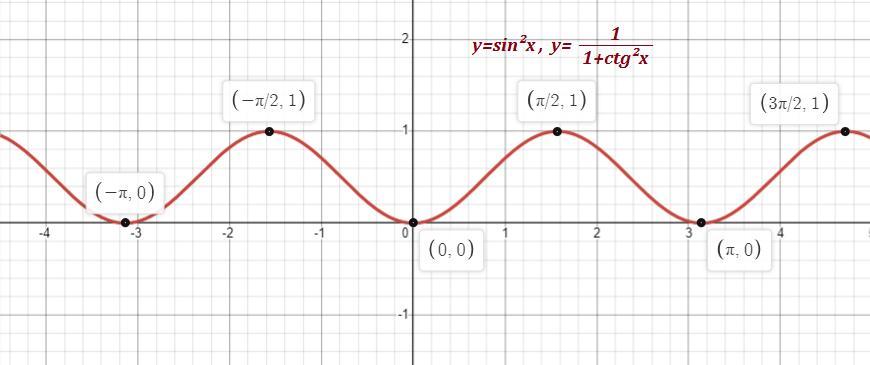
Cтроим график функции .
ООФ:
Известно тождество . Отсюда функцию можно
записать в виде .
Нули функции там же, где и у функции , так как
.
Асимптот функция не имеет . Принимает только неотрицательные значения , множество значений функции: .
Точки экстремума при
Знаки:
Функция возрастает при и убывает при
.
Точки максимума: , точки минимума
.
Приложения:
Похожие вопросы
Предмет: Биология,
автор: hellostendoff7
Предмет: Английский язык,
автор: dimontttop4
Предмет: Українська література,
автор: Marina24121990
Предмет: Русский язык,
автор: bibikkakakaka
Предмет: Математика,
автор: fuwaha