Предмет: Геометрия,
автор: sverd1
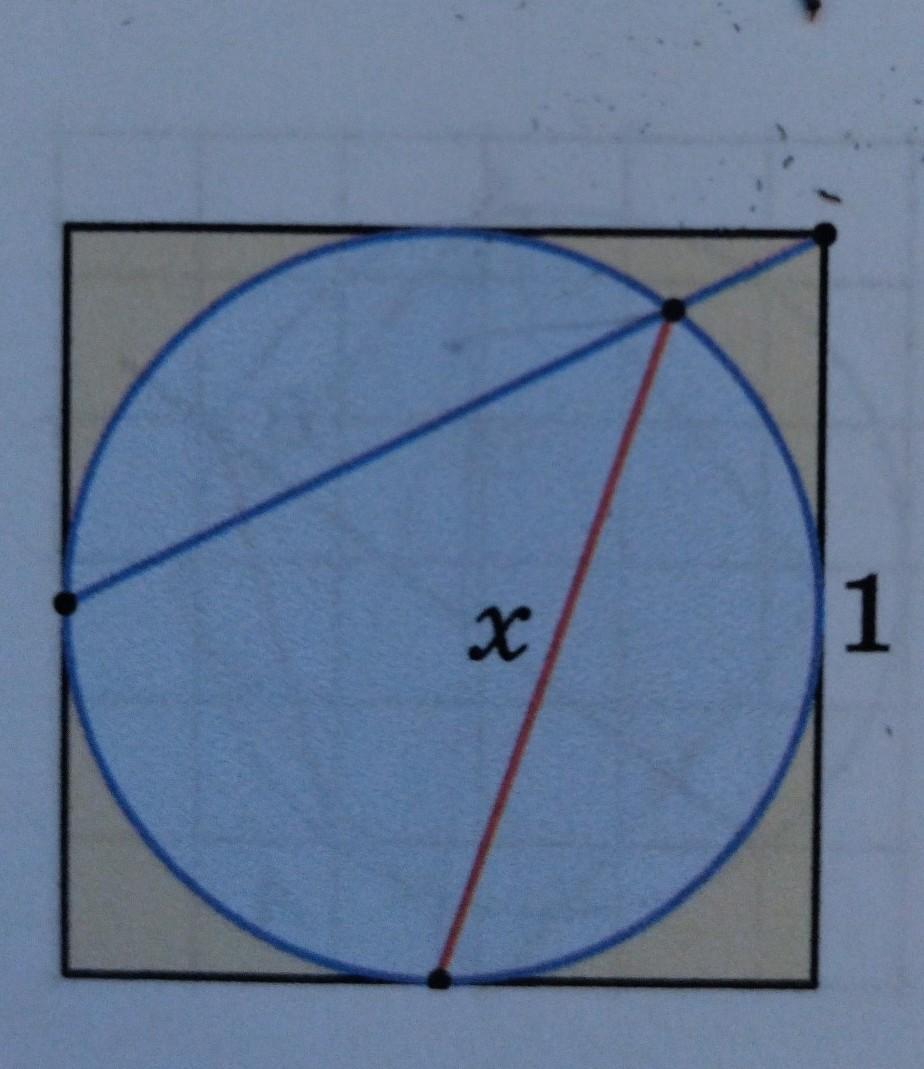
7. ** В квадрат со стороной 1 впи- сана окружность. Найдите длину от- резка, обозначенного на рисунке бук- вой х. (» рис.)
Приложения:
Ответы
Автор ответа:
2
Ответ:
Длина отрезка, обозначенного на рисунке буквой х равна .
Объяснение:
7. ** В квадрат со стороной 1 вписана окружность. Найдите длину отрезка, обозначенного на рисунке буквой х.
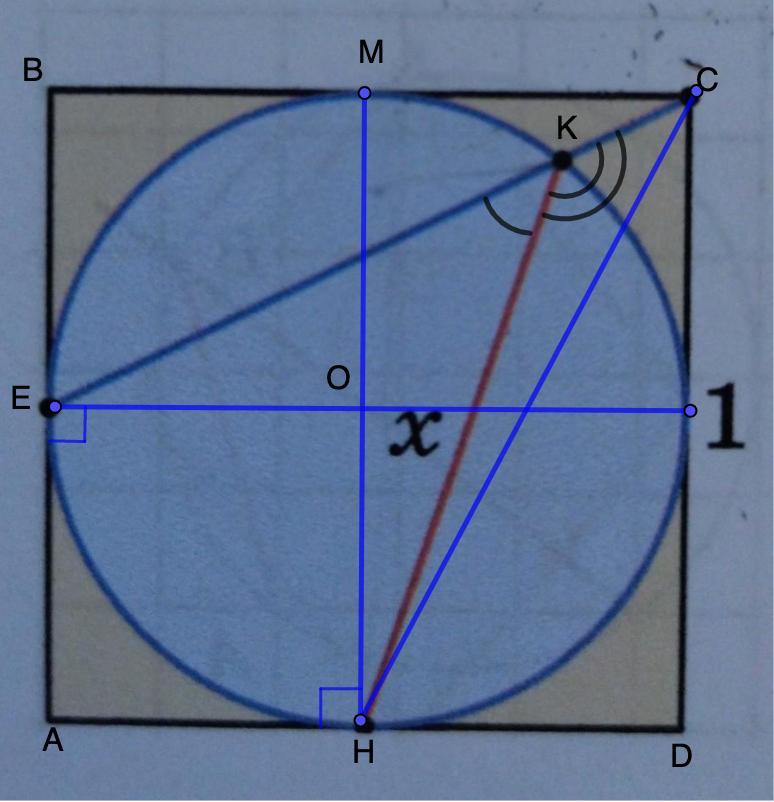
Дано: ABCD - квадрат;
Окр.О - вписана в квадрат;
АВ = 1.
Найти: х.
Решение:
1. Рассмотрим ΔЕВС - прямоугольный.
По теореме Пифагора:
2. Найдем КС.
- Если из одной точки проведены касательная и секущая к окружности, то квадрат расстояния от данной точки до точки касания равен произведению расстояний от этой точки до точек пересечения секущей с окружностью.
⇒ СМ² = ЕС · КС
.
3. Найдем ∠НКС.
- Радиус, проведенный в точку касания, перпендикулярен касательной.
⇒ ОЕ ⊥ АВ; ОН ⊥ AD.
∠ЕОН = 90° - центральный.
- Центральный угол равен градусной мере дуги, на которую он опирается.
⇒ ◡ЕН = 90°
∠ЕКН - вписанный, опирается на ◡ЕН.
- Вписанный угол равен половине градусной мере дуги, на которую он опирается.
⇒ ∠ЕКН = 45°
- Сумма смежных углов равна 180°.
⇒ ∠НКС = 180° - 45° = 135°
4. Рассмотрим ΔЕКС.
- Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
x₂ не подходит по условию задачи.
Длина отрезка, обозначенного на рисунке буквой х равна .
Приложения:
AlexSmithengl:
Добрый день! а есть способ без теоремы косинусов?
Похожие вопросы
Предмет: Қазақ тiлi,
автор: hhja
Предмет: Математика,
автор: kola05454
Предмет: Українська література,
автор: kovtuniakvalentun
Предмет: Литература,
автор: hdhdjdjd73
Предмет: География,
автор: lmuha388