Предмет: Геометрия,
автор: sverd1
Окружность радиуса R вписана * в угол величины а. Из точки её каса- ния с одной из сторон угла на другую его сторону опустили перпендикуляр. Найдите длину хорды окружности, ле- жащей на этом перпендикуляре. (► рис.)
Приложения:
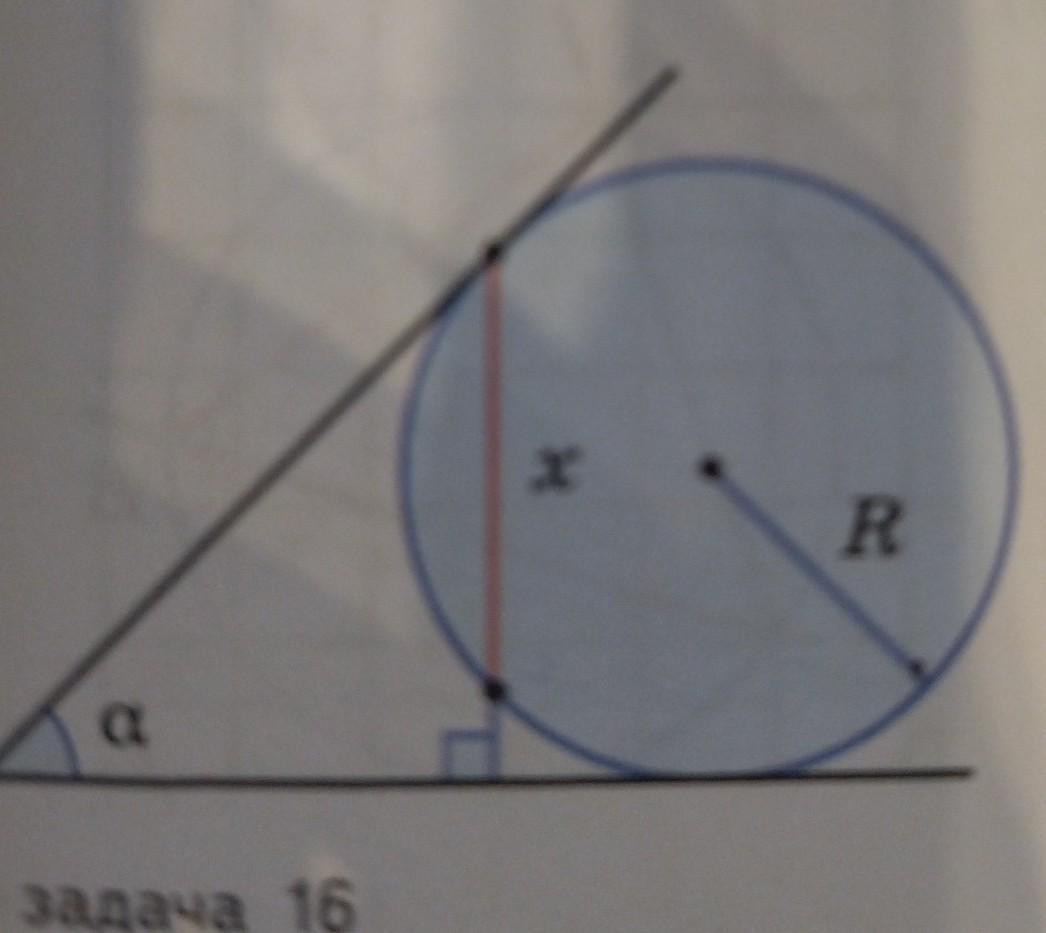
Ответы
Автор ответа:
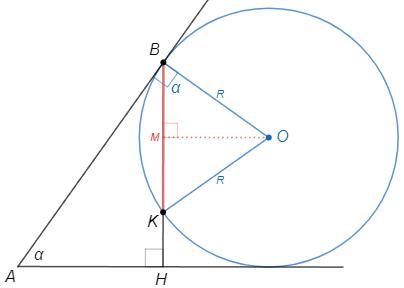
2
OB=OK =R (радиусы)
OM - высота и медиана в △BOK
∠OBM =90°-∠ABH =a
BM =OB cosOBM =R cosa
BK =2BM =2R cosa
Или пусть T - точка на окружности
∠BTK =◡BK/2 =∠ABH (угол между касательной и хордой) =90°-a
=> sinBTK =sin(90°-a) =cosa
BK/sinBTK =2R (т синусов) => BK=2R cosa
Приложения:

sverd1:
без чертежа невозможно понять какая буква это что
Похожие вопросы
Предмет: Математика,
автор: Vika1234448977
Предмет: Қазақ тiлi,
автор: azjhcakwofpd
Предмет: География,
автор: illamihaile
Предмет: Математика,
автор: Аноним