Предмет: Геометрия,
автор: katyakatyaivano
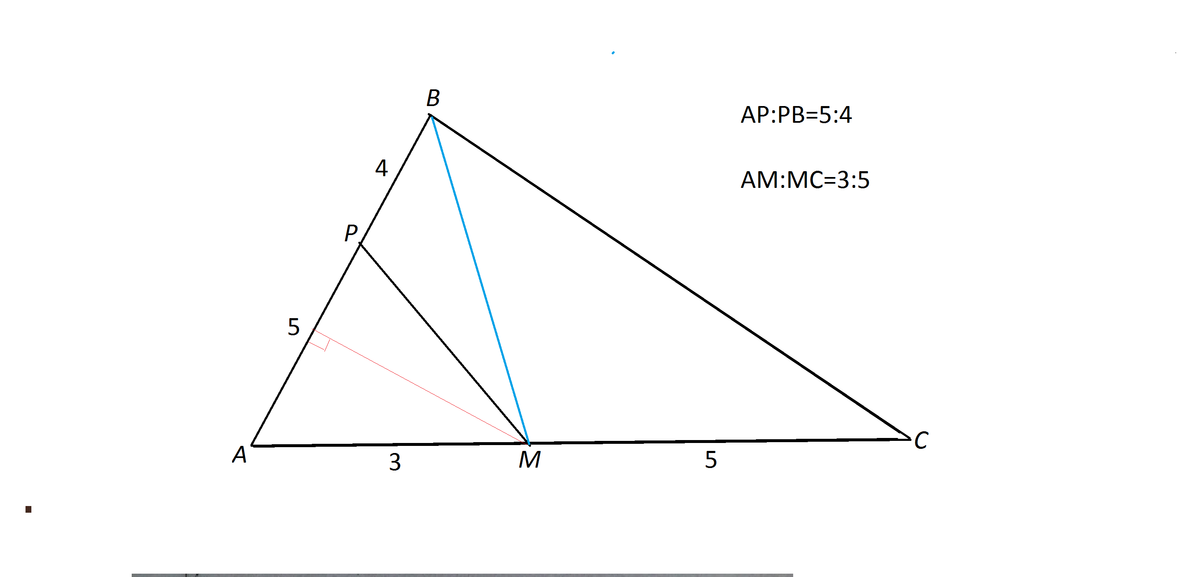
Прямая пересекает стороны AB и AC треугольника ABC в точках P и M соответственно. Найдите отношение площади треугольника APM к площади четырехугольника MCBP, если AP:PB=5:4, AM:MC=3:5.
Ответы
Автор ответа:
0
площадь треугольника APM=1/2*5*3*sinA
площадь треугольника ABC=1/2*(5+4)*(3+5)*sinA
площадь 4хугольника = S abc - S apm = 1/2*(5+4)*(3+5)*sinA - 1/2*5*3*sinA = 1/2*sinA*(9*8-15)
площадь треугольника APM / площадь 4хугольника = (1/2*15*sinA)/(1/2*sinA*(9*8-15)) = 15/(72-15) = 15/57
площадь треугольника ABC=1/2*(5+4)*(3+5)*sinA
площадь 4хугольника = S abc - S apm = 1/2*(5+4)*(3+5)*sinA - 1/2*5*3*sinA = 1/2*sinA*(9*8-15)
площадь треугольника APM / площадь 4хугольника = (1/2*15*sinA)/(1/2*sinA*(9*8-15)) = 15/(72-15) = 15/57
Автор ответа:
0
Вариант решения.
Пусть S - площадь треугольника АВС.
Необходимо найти отношение площадей треугольника АРМ и четырехугольника ВРМС.
Сделаем рисунок и соединим В и М отрезком ВМ.
Отношение площадей треугольников с равными высотами равно отношению их оснований.
Высота ∆ АВМ и ∆ АВС одна и та же.
Основания их относятся как АМ:АС = 3:(3+5) ,
Площадь ∆ АВМ равна 3/8 площади ∆ АВС, т.е. ³/₈S
На том же основании площадь ∆ АРМ равна 5/9 площади ∆ АВМ ( у них одна и та же высота из М к АВ) и равна ⁵/₉ от ³/₈S
Площадь ∆ АРМ=¹⁵/₇₂S=⁵/₂₄S
Площадь четырехугольника ВРМС равна
S(ABC) - ⁵/₂₄(S(ABC) =¹⁹/₂₄ S(∆ ABC)
Площади ∆ АРМ и четырехугольника ВРМС относятся как
(⁵/₂₄S):¹⁹/₂₄ S)=5:19
Пусть S - площадь треугольника АВС.
Необходимо найти отношение площадей треугольника АРМ и четырехугольника ВРМС.
Сделаем рисунок и соединим В и М отрезком ВМ.
Отношение площадей треугольников с равными высотами равно отношению их оснований.
Высота ∆ АВМ и ∆ АВС одна и та же.
Основания их относятся как АМ:АС = 3:(3+5) ,
Площадь ∆ АВМ равна 3/8 площади ∆ АВС, т.е. ³/₈S
На том же основании площадь ∆ АРМ равна 5/9 площади ∆ АВМ ( у них одна и та же высота из М к АВ) и равна ⁵/₉ от ³/₈S
Площадь ∆ АРМ=¹⁵/₇₂S=⁵/₂₄S
Площадь четырехугольника ВРМС равна
S(ABC) - ⁵/₂₄(S(ABC) =¹⁹/₂₄ S(∆ ABC)
Площади ∆ АРМ и четырехугольника ВРМС относятся как
(⁵/₂₄S):¹⁹/₂₄ S)=5:19
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: notdepressed
Предмет: Русский язык,
автор: matveygrebenets
Предмет: Русский язык,
автор: ilvirailvira47
Предмет: Алгебра,
автор: Линка05
Предмет: Математика,
автор: Оля11112