Помогите пожалуйста решить. Буду благодарен.
Ответы
Ответ:
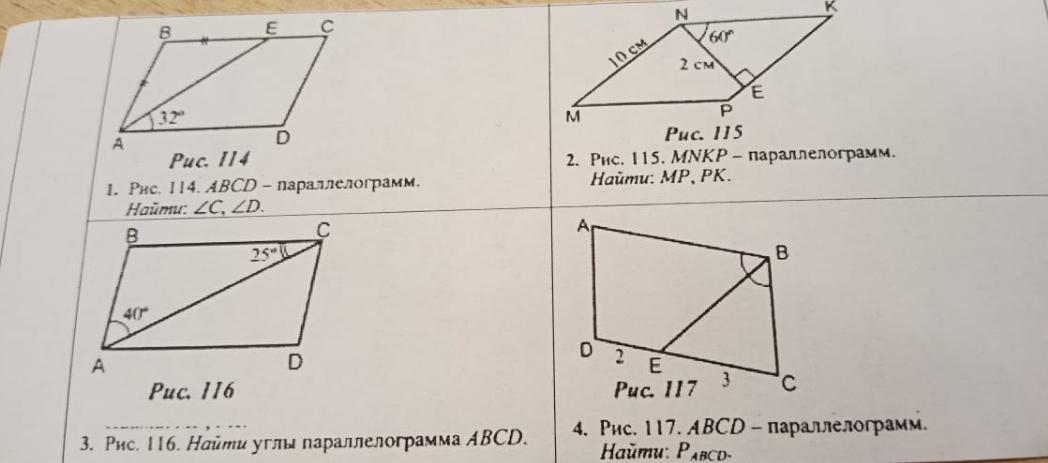
Рис. 114.
Угол EAD=углу ВЕА=32° так как они накрест лежащие при параллельных ВС и АD.
ΔАВС–равнобедренный, значит АЕ–биссектриса угла А. Угол А=32°×2=64°
Так как у параллелограмма противоположные углы равны, то угол С=углу А=64°, а угол В=углу D=180°-64°=116°
Ответ: угол С=64°, угол D=116°
Рис. 115.
Противоположные стороны параллелограмма равны, поэтому MN=PK и MP=NK.
PK = MN = 10см ⇒ PK = 10см.
В ΔNEK: ∠E = 90°; ∠N = 60°; NE = 2см. ∠K = 90° - ∠N = 30° - как острые углы в прямоугольном треугольнике. NK = 2×NE = 2×2см = 4см т.к. NE - катет лежащий напротив угла в 30°.
MP = NK = 4см ⇒ MP = 4см.
Ответ: MP = 4см; PK = 10см.
Рис. 116.
∠САД=25° как накрест лежащий с ∠С=25°
В параллелограмме ∠А=40°+25°=65° его ∠С=∠А=65° как противоположные углы параллелограмма
Ответ: ∠В=∠Д=180°-65°=115°
Рис. 117.
∠АВЕ=∠ВЕС (накр.леж. углы АB||СD, ВЕ–секущая) ⇒ ∆ВЕС–равнобедренный ⇒ ВС=3
DC=DE+EC=5
P=2×(BC+DC)
P=2×(3+5)=16
Ответ: Р=16