Question

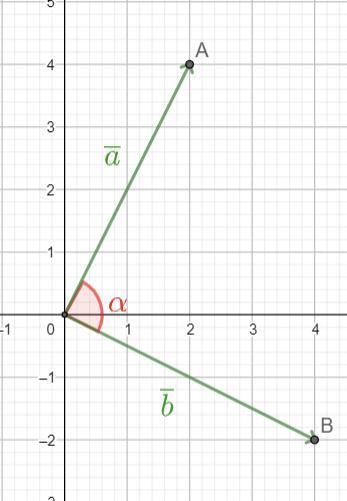
Два пешехода вышли из одного пункта и движутся в разных направлениях. Координаты их места отдыха А(2;4), В (4;-2). Какой угол между данными векторами?​

Answer 1

Ответ:

• Угол между векторами равен α=90°

Объяснение:

Скалярное произведение векторов: $\boxed{\overline a\cdot \overline b = |\overline a|\cdot |\overline b|\cdot \cos \alpha }$, где $\boldsymbol {|\overline a|}$ и $\boldsymbol {|\overline b|}$ - длины векторов, α - угол между векторами.

Из формулы скалярного произведения векторов можно найти угол между векторами.

Найдем cosα:

$\displaystyle \boldsymbol { \cos \alpha} =\frac{\overline a\cdot \overline b}{|\overline a|\cdot |\overline b|} =\frac{x_1\cdot x_2+y_1\cdot y_2}{\sqrt{x_1^2+y_1^2}\cdot \sqrt{x _2^2+y_2^2} } =\frac{2\cdot 4+4\cdot (-2)}{\sqrt{2^2+4^2}\cdot \sqrt{4^2+(-2)^2} } =\frac{0}{20} =\boldsymbol 0$

Тогда угол между векторами α:

$\boldsymbol \alpha =\arccos (0)=\boldsymbol {90^\circ}$

#SPJ1