Question

70. Высота пирамиды равна 4 м и совпадает с одним из боковых ребер. Найдите площадь ее полной поверхности, если основанием пирамиды является: б) равносторонний треугольник со стороной 2 в корне 3 м
​

Answer 1

Ответ:

Площадь полной поверхности равна 16√3 м²

Объяснение:

Дано:

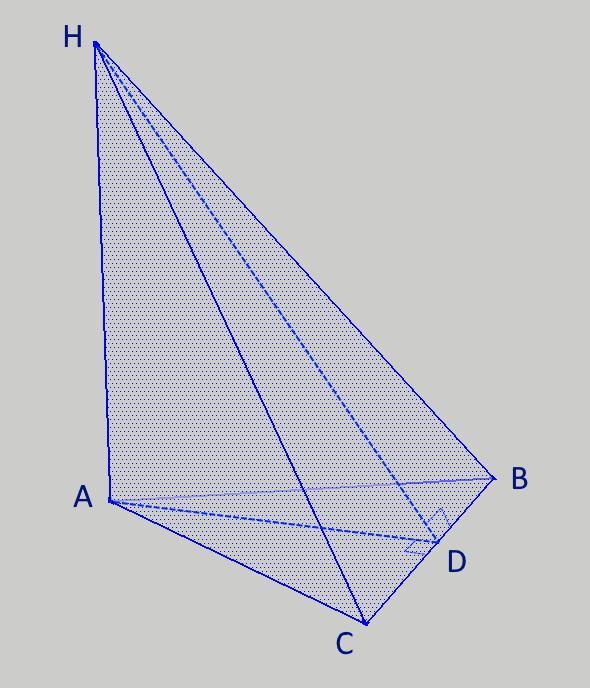
AB = AC = BC = 2√3 м

AH = 4 м

S - ?

-------

Площадь полной поверхности такой пирамиды состоит из площади основания S(ABC) и площадей боковых граней S(ABH), S(ACH), S(BCH)

Проведем высоту основания AD. Высота в равностороннем треугольнике рассчитывается как

$\boxed{h = \dfrac{a \,\root \of {3}} {2} }$

Вычислим:

$AD = \dfrac{AB \,\root \of {3}}{2} = \dfrac{2 \,\root \of {3}\cdot \root \of {3}}{2} = 3$ м

В основании равносторонний треугольник, его площадь равна:

$S(ABC) = \dfrac{AD\cdot BC}{2} = \dfrac{3\cdot 2 \,\root \of {3}}{2} = 3 \,\root \of {3}$ м²

Грани ABH и ACH являются прямоугольными треугольниками с катетами: высотой AH и стороной основания AB и AC. Площади этих граней равные и каждая из них равна:

$S(ABH) = S(ACH) = \dfrac{AH\cdot AB}{2} = \dfrac{4\cdot 2\,\root \of {3}}{2} = 4\,\root \of {3}$ м²

Δ ADH прямоугольный, так как AH перпендикулярна плоскости основания, а следовательно перпендикулярна любой линии этой плоскости: AH⊥AD.

Из треугольника ADH по теореме Пифагора найдем HD:

HD = √(AH²+AD²) = √(4²+3²) = 5 м

По теореме о трех перпендикулярах: прямая, лежащая в плоскости (BC), перпендикулярна наклонной (HD) тогда и только тогда, когда она перпендикулярна проекции этой наклонной (AD) на данную плоскость.

AD⊥BC по построению, AD является проекцией HD на плоскость основания. Поэтому в Δ BCH HD является высотой. Найдем площадь грани S(BCH):

$S(BCH) = \dfrac{HD\cdot BC}{2} = \dfrac{5\cdot 2\,\root \of {3}}{2} = 5\,\root \of {3}$ м²

Площадь полной поверхности равна:

S = S(ABC)+S(ABH)+S(ACH)+S(BCH) = 3√3+4√3+4√3+5√3 = 16√3 м²

Answer 2

Ответ:

$\boldsymbol{\boxed{S_{p} = 16\sqrt{3} }}$ м²

Площадь полной поверхности пирамиды равна $\boldsymbol{16\sqrt{3}}$ м²

Объяснение:

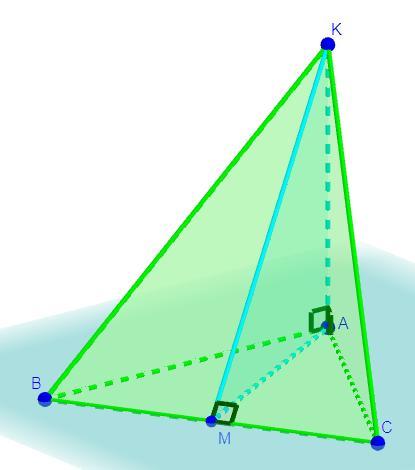
Дано: KA = 4 м, KA - высота, AB = BC = AC = $2\sqrt{3}$ м, KABC - пирамида

Найти: $S_{p} \ - \ ?$

Решение:

Из точки A к стороне BC в точку M проведем высоту AM (AM ⊥ BC) правильного треугольника ΔABC.

По свойствам правильного треугольника (по условию ΔABC - правильный) все его углы равны 60°, тогда угол ∠CAB = 60°.

Так как по условию, KA - высота пирамиды (KABC), то по определению высоты пирамиды, следует что AK ⊥ ABC.

По определению прямая перпендикулярная к плоскости перпендикулярна к любой прямой лежащей в этой плоскости, то так как AK ⊥ ABC, то AK ⊥ (AB,AC,AM), так как (AB,AC,AM) ⊂ ABC,следовательно треугольники ΔKAB,ΔKAC,ΔKAM - прямоугольные.

По формуле площади треугольника (ΔABC):

$\boldsymbol{S_{\Delta ABC}} = \dfrac{AB \cdot AC \cdot \sin \angle CAB}{2} = \dfrac{2\sqrt{3} \cdot 2\sqrt{3} \cdot \sin 60^{\circ}}{2} = \dfrac{2 \cdot 3 \sqrt{3} }{2} \boldsymbol{ = 3 \sqrt{3}}$ м².

$S_{\Delta ABC} = \dfrac{AM \cdot BC}{2} \Longrightarrow \boldsymbol{ AM } =\dfrac{2S_{\Delta ABC}}{BC} = \dfrac{2 \cdot 3\sqrt{3} }{2\sqrt{3} } = \boldsymbol{ 3}$ м.

Рассмотрим прямоугольный треугольник ΔKAM.

По следствию из теоремы Пифагора:

$\boldsymbol{ KM} = \sqrt{AM^{2} + AK^{2}} = \sqrt{3^{2} + 4^{2}} = \sqrt{9 + 16} = \sqrt{25} \boldsymbol{ = 5}$ м.

По теореме о трех перпендикулярах MK ⊥ BC, так как AM ⊥ BC по построению, AK ⊥ MA и AM - проекция отрезка MK на плоскость ABC в прямоугольном треугольнике ΔKAM.

По формуле площади треугольника (ΔBKC):

$\boldsymbol{S_{\Delta BKC}} = \dfrac{MK \cdot BC}{2} = \dfrac{5 \cdot 2\sqrt{3} }{2} \boldsymbol{= 5\sqrt{3}}$ м².

По формуле площади прямоугольного треугольника:

$\boldsymbol{S_{\Delta KAB}} = \dfrac{AK \cdot BA}{2} = \dfrac{4 \cdot 2\sqrt{3} }{2} \boldsymbol{= 4\sqrt{3}}$ м².

$\boldsymbol{S_{\Delta KAC}} = \dfrac{AK \cdot CA}{2} = \dfrac{4 \cdot 2\sqrt{3} }{2} \boldsymbol{= 4\sqrt{3}}$ м².

По определению полной поверхности пирамиды (KABC):

$\boldsymbol{S_{p} }= S_{\Delta ABC} + S_{\Delta BKC} + S_{\Delta KAB} + S_{\Delta KAC} = 3\sqrt{3} + 5\sqrt{3} + 4\sqrt{3} + 4\sqrt{3} \boldsymbol{= 16\sqrt{3}}$ м².