Предмет: Геометрия,
автор: Аноним
помогите пожалуйста люди добрые очень нужно
должно выйти 135 нужно решение( вправа 41)
Приложения:

Ответы
Автор ответа:
1
Ответ:
Наибольший угол треугольника равен 135°.
Объяснение:
Теорема косинусов:
- квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
В треугольнике против большей стороны лежит больший угол.
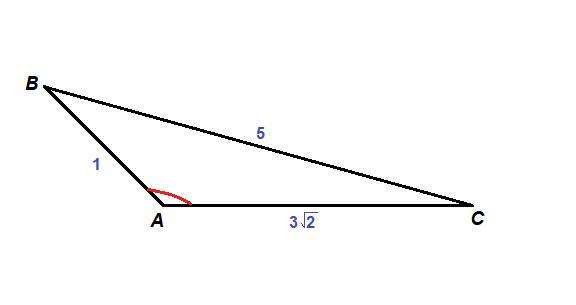
3√2 = √18
5 = √25
Так как √25 > √18, то ВС = 5 - большая сторона треугольника.
∠А лежит против большей стороны, значит он наибольший.
Запишем теорему косинусов для стороны ВС:
BC² = AB² + AC² - 2·AB·AC·cos∠A
∠A = 135°
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: 03monetka03
Предмет: Литература,
автор: iskakovmansur070707
Предмет: Русский язык,
автор: Userhacker
Предмет: Алгебра,
автор: smolhd68
Предмет: Биология,
автор: alinasidorova852