Предмет: Геометрия,
автор: damirriyatov
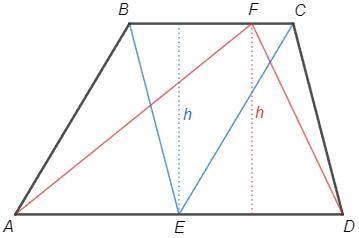
Дана трапеция ABCD с основаниями AD и BC. На стороне AD взяли ее середину E, а стороне BC выбрали произвольную точку F, и оказалось, что площадь треугольника BCE равна 3, а площадь треугольника ADF равна 6. Найдите площадь трапеции.
siestarjoki:
6+3=9
Ответы
Автор ответа:
2
h - высота трапеции
Высоты треугольников BCE и ADF равны h, т.к. расстояние между параллельными постоянно.
S(BCE) =1/2 BC *h =3
S(ADF) =1/2 AD *h =6
S(BCE)+S(ADF) =(BC+AD)h/2 =S(ABCD) =6+3 =9
Приложения:
Похожие вопросы
Предмет: История,
автор: dianalastoveckaa40
Предмет: Математика,
автор: kroma2923
Предмет: Українська мова,
автор: hinkiz
Предмет: Русский язык,
автор: Аноним