Question

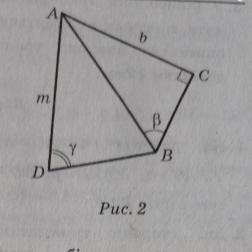
На рисунку 2 AC=b, кутC=90°, кутАBC=B, кут ADB=у
AD = m. Знайдіть синус кута ABD

Answer 1

Ответ:

$\bf \sin\angle ABD = \frac{m \cdot sin \gamma \cdot sin \beta }{b}$

Объяснение:

Дано: AC=b, ∠C=90°, ∠АBC=ß, ∠ADB= , AD = m.

Найти: sin∠ABD

Решение:

1) Рассмотрим прямоугольный треугольник ABC(∠C=90°)

• Синусом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к гипотенузе. 

$\sin \angle ABC= \dfrac{AC}{AB}$

тогда гипотенуза АВ будет равна:

$AB = \dfrac{b}{ \sin \beta }$

2) Рассмотрим треугольник ABD

Теорема синусов:

• Стороны треугольника пропорциональны синусам противолежащих углов.

$\dfrac{AD}{ \sin\angle ABD } = \dfrac{AB}{ \sin \angle ADB }$

Находим sin∠ADB:

$\sin \angle ABD = \dfrac{AD\cdot \sin \angle ADB}{AB} = \dfrac{m\cdot \sin \gamma \sin \beta }{b}$