Предмет: Математика,
автор: Аноним
Здравствуйте! Попрошу решить задачу с номером 5
Приложения:
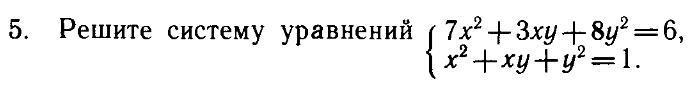
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Приложения:

Автор ответа:
0
Ответ:
Пошаговое объяснение:
пусть , тогда
разделим левую часть на левую, правую на правую (х=0; y=k*0=0 --не решение системы
- потери корней не будет)
или
рассмотрим первый случай
рассмотрим второй случай
Приложения:

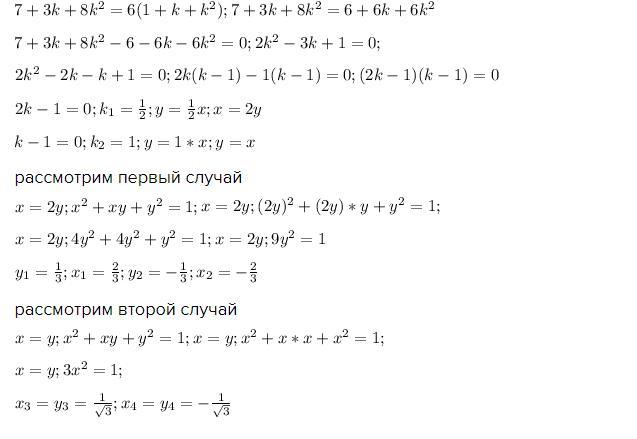
Похожие вопросы
Предмет: Українська мова,
автор: mariaevres81
Предмет: Математика,
автор: vladislavamelnikova2
Предмет: Қазақ тiлi,
автор: aminamakezanova
Предмет: Математика,
автор: 68234586
Предмет: Английский язык,
автор: kotsanvolodimir