Предмет: Математика,
автор: Аноним
Здравствуйте! Попрошу решить задачу с номером 1
Приложения:
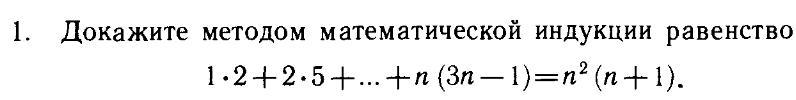
Ответы
Автор ответа:
0
Пошаговое объяснение:
База индукции. При n=1 равенство справедливо
Шаг индукции. Пусть равенство справедливо при n=k, т.е.
верно равенство
докажем, что тогда оно справедливо при n=k+1, т.е. что тогда верное равенство
Рассмотрим сумму
используя гипотезу индукции, перепишем в виде
путем преобразований пришли к тому что и требовалось доказать.
Согласно методу математической индукции утверждение верно. Доказано
Приложения:

Похожие вопросы
Предмет: Геометрия,
автор: annacat201911
Предмет: Українська мова,
автор: annakarpenko799
Предмет: Математика,
автор: ksbushueva13
Предмет: Русский язык,
автор: MrLeon321
Предмет: Русский язык,
автор: arushon086