Question

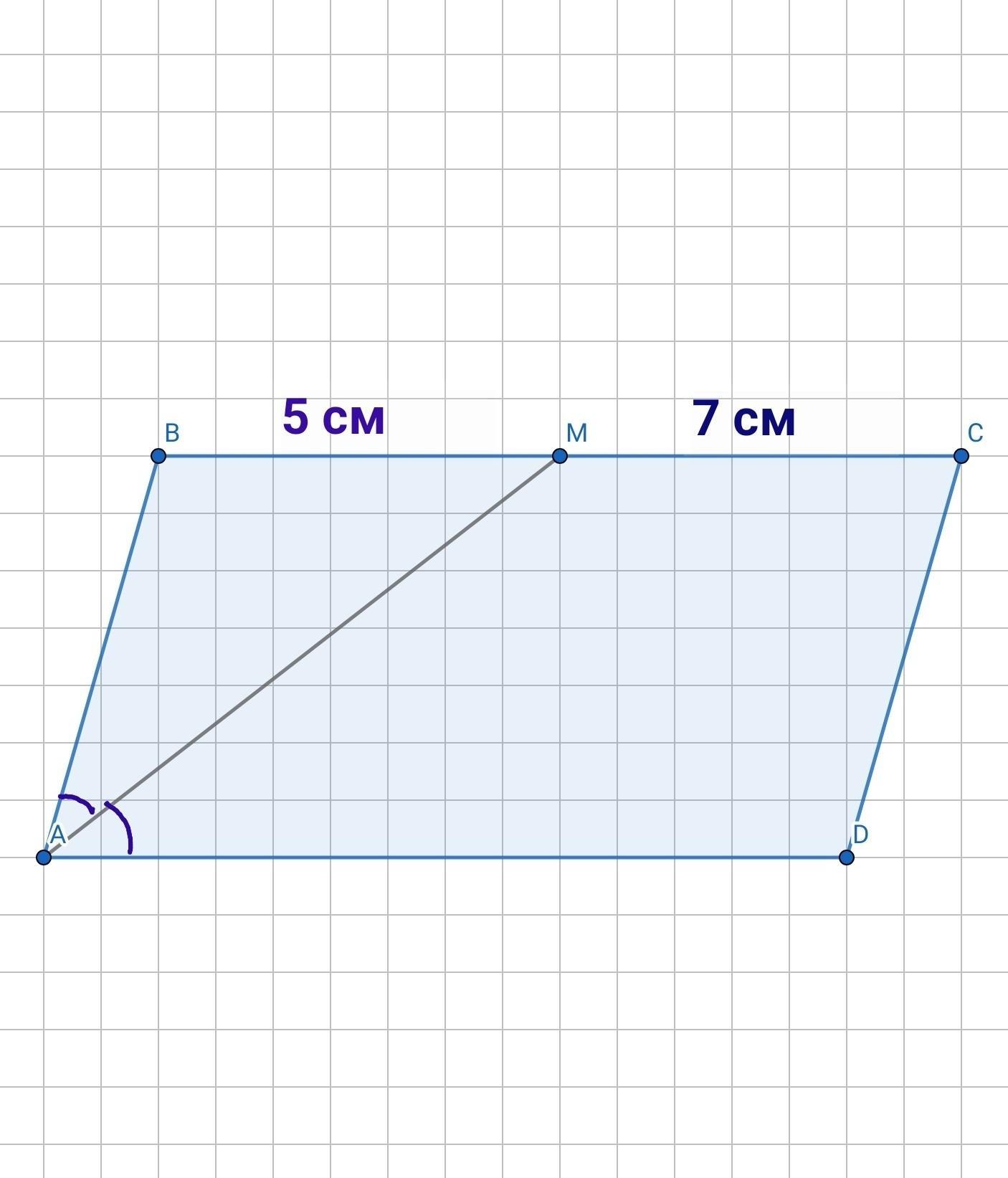
56. У паралелограмі ABCD бісектриса кута А ділить сторону ВС на відрізки BM = 5 см і МС = 7 см. Знайдіть периметр паралелограма.
​

Answer 1

Объяснение:

У паралелограмі ABCD бісектриса кута А ділить сторону ВС на відрізки BM = 5 см і МС = 7 см. Знайдіть периметр паралелограма.

• Паралелограм - це чотирикутник у якого протилежні сторони попарно паралельні та рівні.
• Периметр паралелограма:

$\boxed {\bf P_{ABCD} = 2(AB + BC)}$

Дано: АВСD - паралелограм, АМ - бісектриса, ∠MAD=∠MAB, BM=5 см, МС =7 см

Знайти: Периметр ABCD.

Розв'язання

1) ВС=ВМ+МС=5+7= 12(см)

2) ∠MAD=∠BMA - як внутрішні різносторонні кути при перетині паралельних прямих AD і BC січною АМ.

∠МАD=∠MAB - за умовою (бісектриса АМ ділить кут А навпіл ), тому ∠BMA=∠MAB.

Отже, за ознакою рівнобедреного трикутника: △АВМ - рівнобедрений,

АВ=ВМ= 5 см

3) Знайдемо периметр:

$\bf P_{ABCD}=2(5+12)=2×17=\bf 34$ (см)