Question

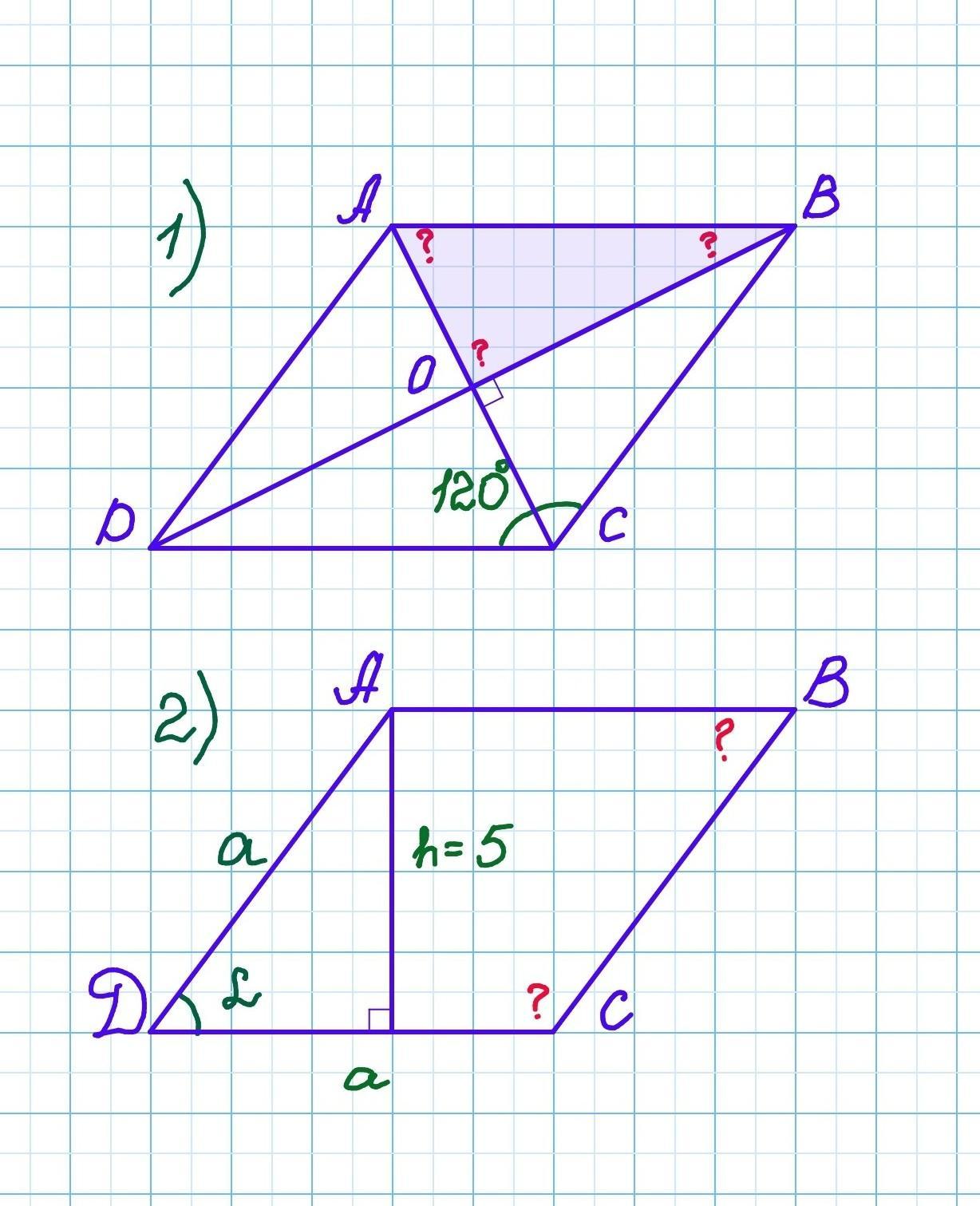
1) У ромбі ABCD відомо, що кут С дорівнює 120 градусів, а діагоналі перетинаються в точці О. Знайдіть кути трикутника АОВ. 2) Знайдіть кути ромба, якщо його периметр дорівнює 40 см, а висота - 5см.

СПАМ-БАН
ПОМОГИТЕ ОЧЕНЬ СРОЧНО
ДАБ 50 БАЛЛОВ ​

Answer 1

Ответ:

1) 60°, 90°, 30°

2) 30°, 30°, 150°, 150°

Объяснение:

• Ромб - це паралелограм, у якого всі сторони рівні.
• Протилежні кути ромба рівні.
• Діагоналі ромба перетинаються під прямим кутом, точка перетину є серединою кожної діагоналі.
• Діагоналі ромба є бісектрисами кутів, з яких вони проведені.
• Сума кутів, що прилягають до однієї сторони дорівнює 180°.

1) У ромбі ABCD відомо, що кут С дорівнює 120 градусів, а діагоналі перетинаються в точці О. Знайдіть кути трикутника АОВ.

∠А=∠С=120° - як протилежні кути ромба.

∠DAC=∠CAB=∠A:2=60° - так як діагональ АС є бісектрисою кута А.

Розглянемо △АОВ.

∠ОАВ=60°.

∠АОВ=90° - так як діагоналі ромба перетинаються під прямим кутом. ⇒ △АОВ - прямокутний.

∠АВО=90°-∠ОАВ=90°-60°=30° - так як сума кутів прямокутного трикутника дорівнює 90°.

2) Знайдіть кути ромба, якщо його периметр дорівнює 40 см, а висота - 5см.

Периметр - це сума всіх сторін ромба. У ромба всі сторони рівні, тому периметр буде дорівнювати:

Р=4•а.

За умовою периметр дорівнює 40 см, знайдемо сторону а:

4•а=40; а =40:4= 10 см

Площа ромба обчислюється за формулами:

(1) S=a•h

(2) S=a²•sinα

а- сторона ромба, h - висота, α - кут між сторонами.

Прирівняємо (1) і (2):

а•h=a²•sinα,

тоді:

$sin \alpha = \dfrac{ah}{ {a}^{2} } = \dfrac{h}{a}$

$sin \alpha = \dfrac{5}{10} = \dfrac{1}{2}$

α=30°

Гостри кути ромба(∠В=∠D) дорівнюють 30°.

Оскільки сусідні кути ромба в сумі дають 180°, а протилежні кути рівні, маємо, що тупі кути ромба:

∠А=∠С=180°-30°=150°.