Question

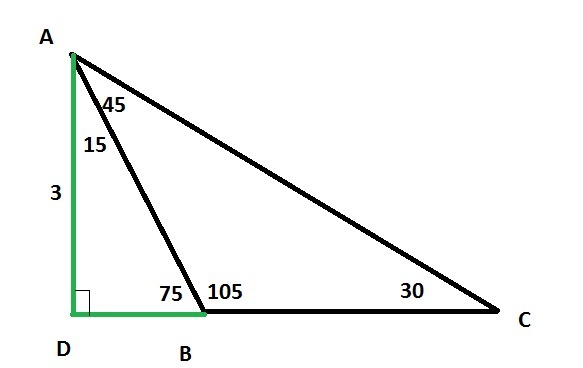
в треугольнике ABC углы A и C равны 45 30 соответственно а высота АД 3 м

найдите стороны

Answer 1

Дано:

∠A=45° , ∠C=30° . AD ⊥ BC , AD = 3 м

AB, BC, AC - ?

Из ΔADC(∠ADC=90°) , катет, который лежит против угла 30° равен половине гипотенузы. AC=2AD=2*3=6м

Сумма углов треугольника = 180° . ∠B=180°-(45°+30)°=105°

$sin105^{circ}=sin(135^{circ}-30^{circ})=sin135^{circ}cos30^{circ}-cos135^{circ}sin30^{circ}=\\=frac{sqrt{2}}{2}*frac{sqrt{3} }{2}+frac{sqrt{2} }{2}*frac{1}{2}=frac{sqrt{6} }{4}+frac{sqrt{2} }{4}=frac{sqrt{6}+sqrt{2}}{4}$

По теореме синусов найдём BC :

$frac{BC}{sin45^{circ}}=frac{AC}{sin105^{circ}}\\frac{BC}{frac{sqrt{2} }{2} }=frac{6}{frac{sqrt{6}+sqrt{2}}{4}}\\BCsqrt{2}=frac{24}{sqrt{6}+sqrt{2}}\\BCsqrt{2}=6(sqrt{6}-sqrt{2})\\BC=frac{6sqrt{6}-6sqrt{2}}{sqrt{2}}=6sqrt{3}-6$

Найдём AB:

$frac{AB}{sin30^{circ}}=frac{BC}{sin45^{circ}}\\frac{AB}{frac{1}{2} }=frac{6sqrt{3}-6 }{frac{sqrt{2} }{2} }\\2AB=frac{12sqrt{3}-12 }{sqrt{2} }\\2AB=frac{2sqrt{2}(6sqrt{3}-6)}{2}\\2AB=6sqrt{6}-6sqrt{2}\\AB=3sqrt{6}-3sqrt{2}$

Ответ: AC = 6м , AB = $3sqrt{6}-3sqrt{2}$ м , BC = $6sqrt{3}-6$ м