Question

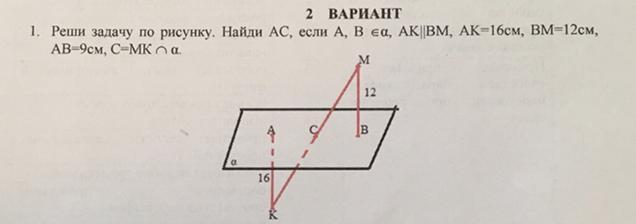
1. Реши задачу по рисунку. Найди AC, если A, B принадлежит a, AK||BM, AK = 16 см, BM = 12 см, AB = 9 см, C = MK дуга a.

Дескриптор:

Применяет свойство параллельных прямых - 1 балл

Доказывает подобие треугольников - 1 балл

Составляет пропорцию соответственных сторон - 1 балл

Находит длину неизвестного отрезка - 1 балл

Answer 1

Ответ:

АС = $5\frac{1}{7}$ см

Объяснение:

Найди AC, если A, B принадлежит α, AK||BM, AK = 16 см, BM = 12 см, AB = 9 см, C = MK∩α.

• Через две параллельные прямые можно провести плоскость, и притом только одну.

Свойство параллельных прямых:

• Если две прямые параллельны то при пересечении их с третьей (секущей) накрест лежащие углы равны.

• Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Основное свойство пропорции:

• Произведение крайних членов пропорции равно произведению средних членов этой пропорции.

РЕШЕНИЕ

МК пересекает α в точке С.

Параллельные АК и МВ лежат в одной плоскости, которая пересекает плоскость α по прямой АВ. Т.е. точки А, С, В лежат на одной прямой.

Рассмотрим ΔАСК и ΔВСМ.

У них:

• ∠АСK=∠ВСМ - как вертикальные

• ∠АКС=∠ВМС - как накрест лежащие углы, образованные при пересечении  параллельных прямых АК и ВМ секущей МК.

Следовательно ΔАСК подобен ΔВСМ по двум углам (первый признак подобия)

Из подобия треугольников следует пропорциональность соответствующих сторон:

$\bf \dfrac{AC}{BC} =\dfrac{AK}{BM}$

Пусть АС= х см, тогда ВС=АС-х= 9-х (см), тогда:

$\dfrac{x}{9-x} =\dfrac{ 16}{12}$

Воспользовавшись свойством пропорций, находим х:

12x=16(9-x)

28x=144

$x=\dfrac{144}{28} =\bf 5\frac{1}{7}$

Таким образом АС =   $\bf 5\dfrac{1}{7}$  см

#SPJ1