Question

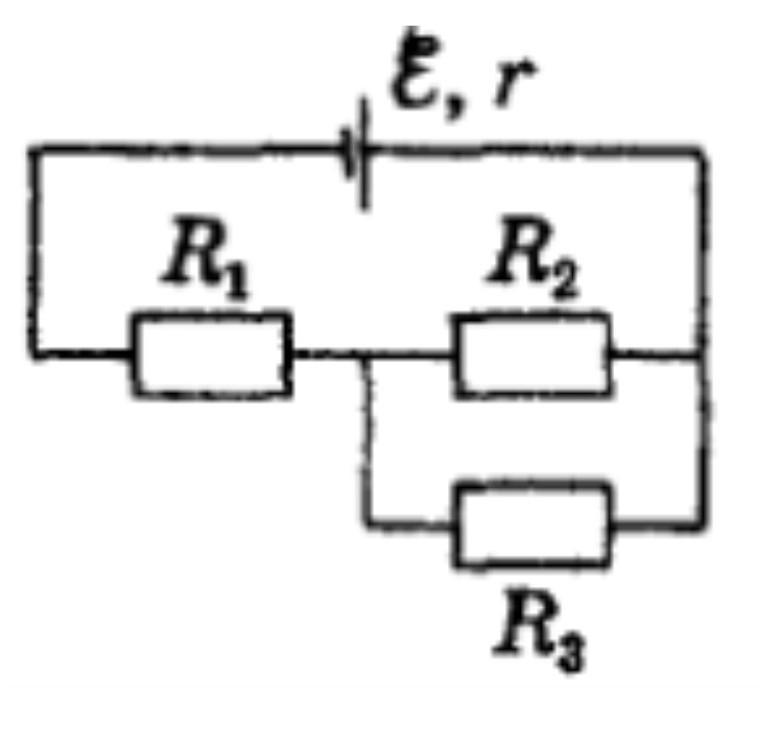
EPC джерела струму 36 В, внутрішній опір 1 Ом. Опір кожного резистора 4 Ом. Знайдіть розподiл електричних струмів та напругу на кожному з резисторів.
​

Answer 1

Ответ:

Сила тока на первом резисторе равна приблизительно 5,14 A, а напряжение приблизительно 20,57 В.

На резисторах 2 и 3 напряжение приблизительно 10,29 В, а сила тока приблизительно 2,57 A

Объяснение:

Дано:

$\xi =$ 36 В

$r =$ 1 Ом

$R_{1} = R_{2} = R_{3}=$ 4 Ом

Найти:

$I_{1} , I_{2}, I_{3} \ - \ ?$

$U_{1} , U_{2}, U_{3} \ - \ ?$

--------------------------------------

Решение:

По законам последовательного соединение резисторов:

$R = R_{1} + R_{2} + \dots + R_{n}$

$U = U_{1} + U_{2} + \dots + U_{n}$

$I = I_{1} = I_{2} = \dots = I_{n}$

По законам параллельного соединение резисторов:

$\displaystyle \frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \dots + \frac{1}{R_{n}}$

$U = U_{1} = U_{2} = \dots = U_{n}$

$I = I_{1} + I_{2} + \dots + I_{n}$

По закону Ома для участка цепи:

$I = \dfrac{U}{R} \Longrightarrow U = IR$

Резисторы 2 и 3:

$\displaystyle \frac{1}{R_{23}} = \frac{1}{R_{2}} + \frac{1}{R_{3}} = \dfrac{R_{3} + R_{2}}{R_{2}R_{3}} \Longrightarrow R_{23} = \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}$

Полное сопротивление цепи:

$R = R_{1} + R_{23} = R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}$

По закону Ома для полной цепи:

$I = \dfrac{\xi}{R + r} = \dfrac{\xi}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}}$

Резистор 1:

$I_{1} = I = \dfrac{\xi}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}}$

$U_{1} = I_{1}R_{1} = \dfrac{\xi R_{1}}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}}$

Напряжение на элементе питания:

$U_{r} = Ir = \dfrac{r\xi}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}}$

На резисторах 2 и 3 напряжение одинаково, так как они соединены параллельно

$\xi = U_{1} + U_{23} + U_{r} \Longrightarrow U_{23} = \xi - U_{1} - U_{r} =$

$=\xi - \dfrac{\xi R_{1}}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}} - \dfrac{r\xi}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}}$

$U_{2} = U_{3} = U_{23} =\xi - \dfrac{\xi R_{1}}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}} - \dfrac{r\xi}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}}$

Ток на резисторе 2:

$I_{2} = \dfrac{U_{2}}{R_{2}} = \dfrac{\xi - \dfrac{\xi R_{1}}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}} - \dfrac{r\xi}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}}}{R_{2}}$

Ток на резисторе 3:

$I_{3} = \dfrac{U_{3}}{R_{3}} = \dfrac{\xi - \dfrac{\xi R_{1}}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}} - \dfrac{r\xi}{r + R_{1} + \dfrac{R_{2}R_{3}}{R_{3} + R_{2}}}}{R_{3}}$

Расчеты:

$\boldsymbol I =$ (36 В) / (1 Ом + 4 Ом + (4 Ом · 4 Ом / (4 Ом + 4 Ом))) $\boldsymbol \approx$ 5,14 A

$I =\ \boldsymbol{ I_{1} \approx}$ 5,14 A

$\boldsymbol{U_{1}} =$ (36 В) / (1 Ом + 4 Ом + (4 Ом · 4 Ом / (4 Ом + 4 Ом))) · 4 Ом $\boldsymbol \approx$

$\boldsymbol \approx$ 20,57 В

$U_{r} =$ 1 Ом · 5,14 A = 5,14 В

$\boldsymbol{U_{2} = U_{3}} =$ 36 В - 20,57 В - 5,14 В $\boldsymbol \approx$ 10,29 В

$\boldsymbol{I_{2}} =$ 10,29 В / 4 Ом $\boldsymbol \approx$ 2,57 A

$\boldsymbol {I_{3}} =$ 10,29 В / 4 Ом $\boldsymbol \approx$ 2,57 A

Ответ: $I_{1} \approx$ 5,14 A. $U_{1} \approx$ 20,57 В. $U_{2} = U_{3} \approx$ 10,29 В. $I_{2} = I_{3} \approx$ 2,57 A.