Предмет: Геометрия, автор: kimkarina953

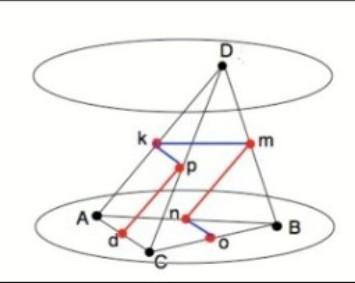
Даны четыре точки A B C D не лежащие в одной плоскости. Докажите,что любые две из трех прямых,соединяющие середины отрезков AB и CD,AC и BD, AD и BC,лежат в одной плоскости.

напишите дано решение по аксиоам если есть

volna7: 4 точки, не лежащие в одной плоскости образуют пирамиду с треугольником в основании. Прямые, соединяющие середины ребер пирамиды лежат на гранях этой пирамиды ( через грань пирамиды можно провести плоскость, так как грань пирамиды - треугольник, а через три точки можно провести плоскость ). Если прямые лежат на разных гранях, но у них одна общая точка, то они образуют ломаную, содержащую три точки, а через них можно провести плоскость.

volna7: Через любые две из трех прямых dp, km, no на рисунке из ответа внизу провести плоскость невозможно.