Question

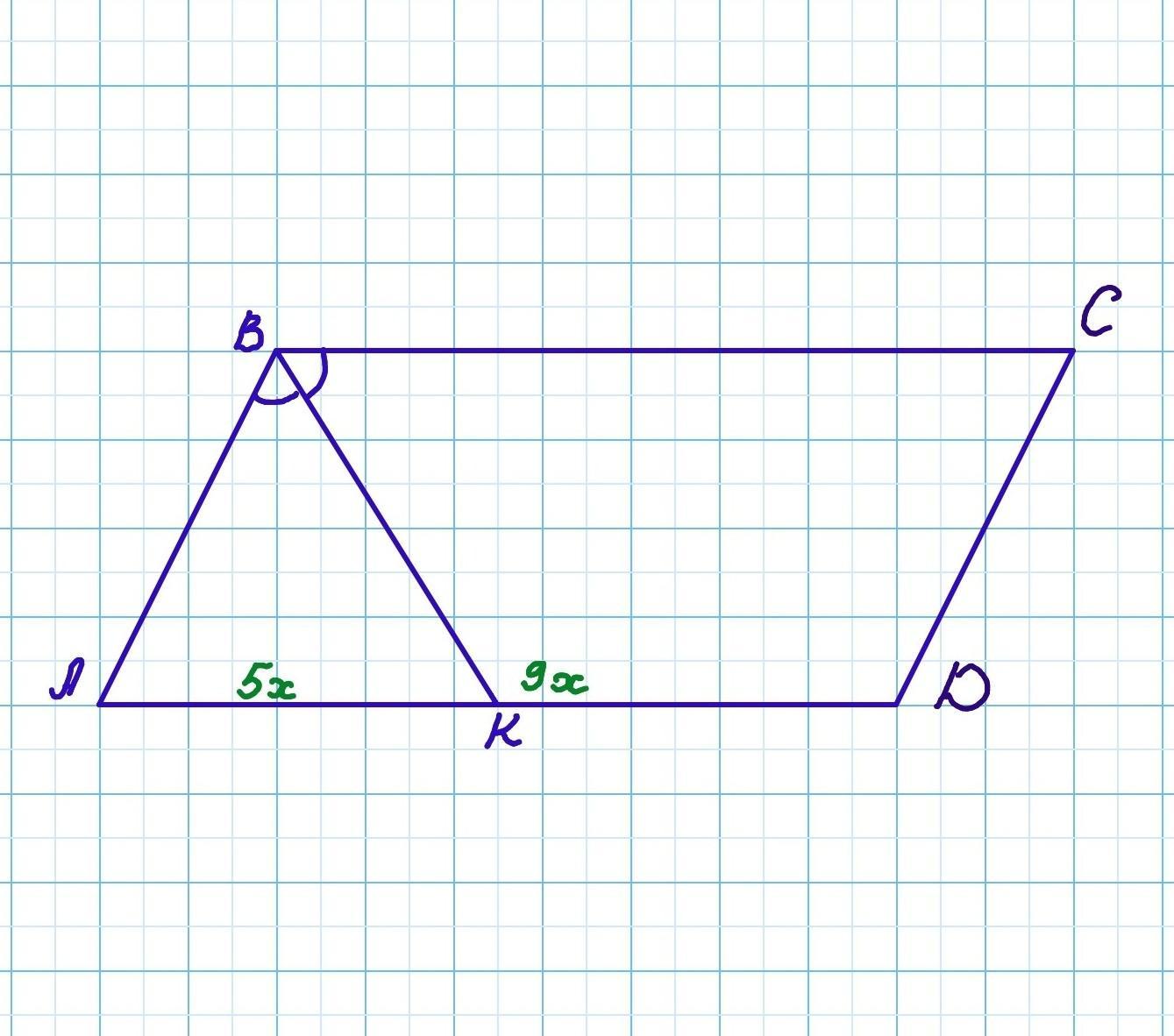
бісектриса кута паралелограма ділить його сторону у відношенні 5:9 , починаючи від найближчої до цього кута вершини знайдіть меншу сторону паралелограма, якщо його периметр дорівнює 38 см

Answer 1

Ответ:

Менша сторона паралелограма дорівнює 5 см

Объяснение:

Бісектриса кута паралелограма ділить його сторону у відношенні 5:9 , починаючи від найближчої до цього кута вершини знайдіть меншу сторону паралелограма, якщо його периметр дорівнює 38 см

• Паралелограм - це чотирикутник у якого протилежні сторони попарно паралельні та рівні.

• Периметр паралелограма:

$\boxed {\bf P_{ABCD} = 2(AB + AD)}$

Дано: АВСD - паралелограм, ВК - бісектриса, ∠ABK=∠KBC, AK:KD=5:9, P(ABCD) = 38 см

Знайти: меншу сторону ABCD.

Розв'язання

1) Нехай AK =5x, тоді KD=9x. AD=AK+KD=5х+9х=14х

2) ∠AKB=∠КBС - як внутрішні різносторонні кути при перетині паралельних прямих AD і BC січною BK.

∠ABK=∠KBC - за умовою (властивість бісектриси), тому ∠AKB=∠ABK.

Отже, за ознакою рівнобедреного трикутника: △АВK - рівнобедрений, з основою АВ.

⇒ АВ=АК=5х

3) Знайдемо периметр:

$P_{ABCD} = 2(5x + 14x) = 2 \times 19x = 38x$

За умовою периметр дорівнює 38 см, складаємо рівняння:

38х=38

х=1

АВ=5•1=5 (см); AD=9•1= 9 (см).

Менша сторона паралелограма дорівнює 5 см