Question

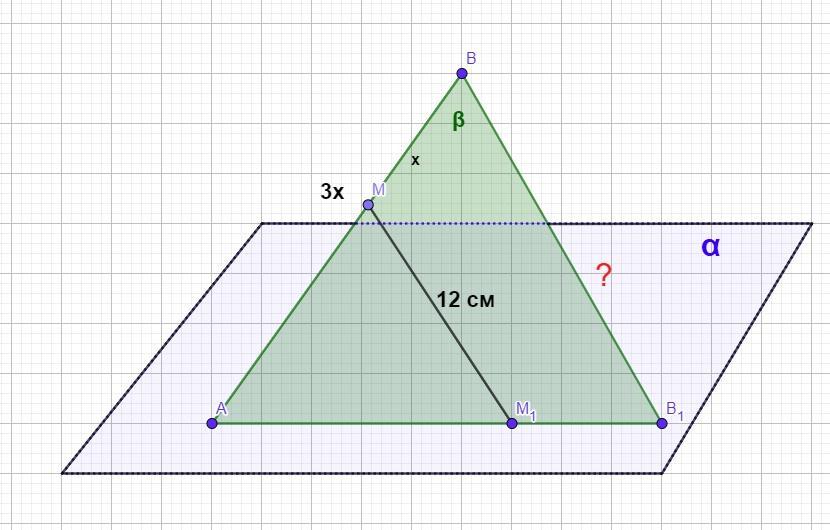
Через кінець А вiдрiзка АВ проведено площину а. Через кінець В і точку М цього вiдрiзка проведено паралельнi прямi, якi перетинають площину а вiдповiдно в точках М. і В.. Знайти довжину вiдрiзка ВВ1, якшо AB: BM=3:1, ММ = 12 см.

Answer 1

Ответ:

ВВ₁ = 18 см

Пошаговое объяснение:

Через кінець А вiдрiзка АВ проведено площину а. Через кінець В і точку М цього вiдрiзка проведено паралельнi прямi, якi перетинають площину а вiдповiдно в точках М. і В.. Знайти довжину вiдрiзка ВВ1, якшо AB: BM=3:1, ММ = 12 см

За умовою задачі маємо відрізок АВ, площину α і пряму ВВ₁, точка В₁ якої належить площині α. Через пряму ВВ₁ і точку А, що не лежить на ній, за властивістю, проведемо площину АВВ₁ (β). ММ₁║ВВ₁ - за умовою, точка М₁ належить площині α. Тому, за теоремою про паралельність прямих у просторі, пряма ММ₁ належить площині АВВ₁ (β). Звідси слідує, що точка М₁ належить відрізку АВ₁, прямої перетину площин α і АВВ₁ (β).

Розглянемо трикутники АВВ₁  і АММ₁ .

У них:

• ∠ВАВ₁ =∠МАМ₁ як спільний кут при вершині А;

• ∠АВВ₁=∠АММ₁  - як відповідні кути при паралельних прямих ВВ₁  і ММ₁ та січній АВ.

Звідси слідує, що за ознакою подібності за двома кутами, трикутники  АВВ₁  і АММ₁ подібні, а значить їх відповідні сторони пропорційні:

$\dfrac{AB}{AM} =\dfrac{BB_1}{MM_1}$

Оскільки, за умовою задачі, АВ:BM=3:1, , то нехай ВМ=х, тоді АВ=3х ⇒ АМ=АВ-ВМ=3х-х=2х . MM₁ = 12 см.

Звідси отримаємо:

$\dfrac{3x}{2x} =\dfrac{BB_1}{12}$

$BB_1=\dfrac{3x*12}{2x} =18$

Отже ВВ₁ = 18 см