Предмет: Алгебра,
автор: kamilmatematik100504
Решите только 27 номер
Приложения:
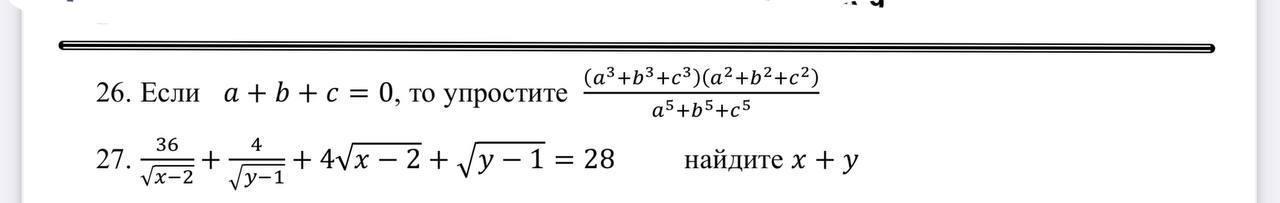
Ответы
Автор ответа:
1
Ответ:
16.
Объяснение:
Как известно (неравенство Коши), среднее арифметическое двух положительных чисел больше или равно среднего геометрического, причем неравенство превращается в равенство тогда и только тогда, когда эти числа равны:
Поэтому
а у нас левая часть должна быть равна 28, поэтому
kamilmatematik100504:
сейчас про треугольники задам задачу , если будет интересно можете решить пожалуйста
Похожие вопросы
Предмет: Математика,
автор: aassiiyyaamukasheva
Предмет: Химия,
автор: Alenanedelcheva
Предмет: Русский язык,
автор: fedorbashlykov
Предмет: Химия,
автор: zaxarenckogosha
Предмет: Геометрия,
автор: kotdasha62