Question

Очень надо помогите пожалуйста на фото задание

Answer 1

Ответ:

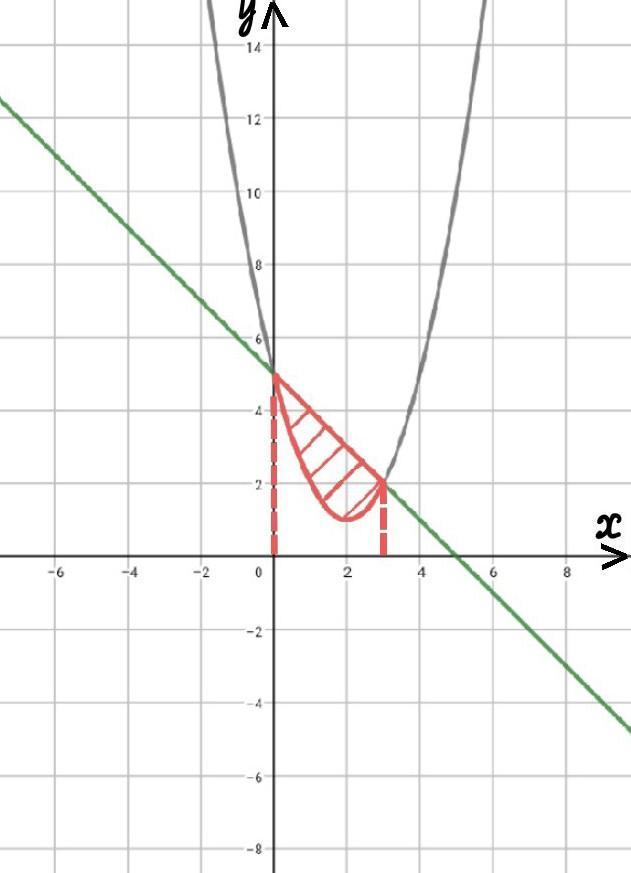
a)График построен

б)Площадь  фигуры , ограниченной данными линиями, равна 4,5(ед)²

Пошаговое объяснение:

y = x² - 4x + 5  ;  y = 5 - x

а) Построим графики функций .

y = x² - 4x + 5

Данная функция квадратичная , графиком является - парабола.

Найдём её вершину :

$\displaystyle x_{v}=\frac{4}{2} =2$

$\displaystyle y_{v}=2^2-4\cdot 2+5=4-8+5=1$

Вершина в точке (2;1)

Возьмём дополнительные точки:

x = 0 ⇒ y = 0²-4·0+5 = 5

x = 1 ⇒ y = 1²-4·1+5 = 2

Поставили точки , по ним провели ветви параболы.

Внимание к линейной функции y = 5 - x

Найдём точки пересечения графиков данных функций

Для начала находим  абсциссу точек пересечения графиков:

$x^2-4x+5=5-x\\x^2-4x+x=0\\x^2-3x=0\\x(x-3)=0\\x_1=0~~~~~~x_2=3$

Значит , график линейной функции пересекается с графиком квадратичной функции в точках (0;5) и (3;2). Предел нашего интегрирования ( 0 ; 3 )  , на данном промежутке функция y = 5 - x расположена выше , чем y = x² - 4x + 5 , следовательно , при интегрировании - от второй функции отнимем первую.

$\displaystyle \int\limits^3_0 {5-x-(x^2-4x+5)} \, dx= \int\limits {-x-x^2+4x} \, dx =\int\limits {3x-x^2} \, dx= \\=3\cdot \frac{x^{1+1}}{1+1} -\frac{x^{2+1}}{2+1} =\frac{3x^2}{2} -\frac{x^3}{3} \Bigg | ^3_0=\frac{3\cdot 3^2}{2} -\frac{3^3}{3}-\Bigg(\frac{3\cdot 0^2}{2} -\frac{0^3}{3} \Bigg)=\frac{27}{2} -9-0=\bf4,5(ed)^2$