Question

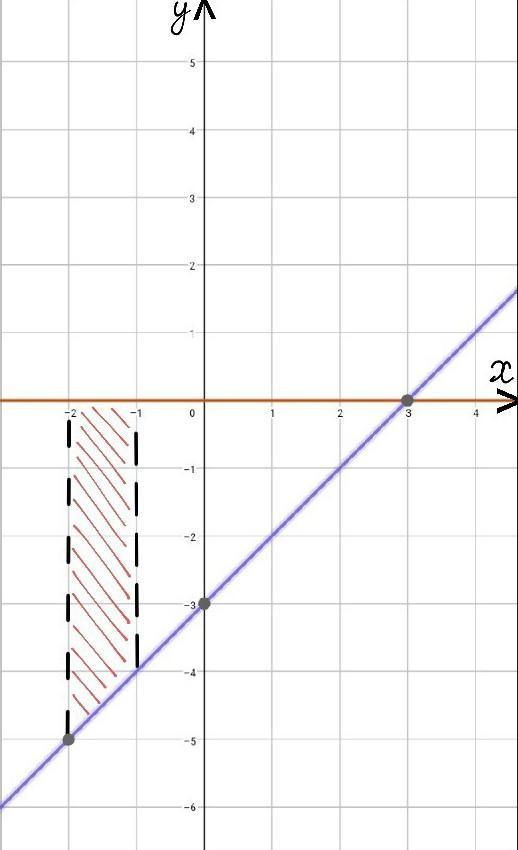
обчислити площу фігури обмеженої графіками функцій y=0; y=x-3; x=-1; x=-2

Answer 1

Ответ:

4,5  (ед)²

Объяснение:

Вычислите площадь фигуры ограниченой графиками функций y = 0 ; y = x - 3 ; x = -1 ; x = -2

1 вариант.  

График функции y = 0 совпадает с осью абсцисc , тогда , построим график линейной функции у = х - 3

Подберём точки :

x = 0 ⇒ y = -3

x = -2 ⇒ y = -5

Третья точка пусть будет точкой пересечения графиков, найдём её:

0 = x - 3

x = 3

Графики пересекаются в точке ( 3 ; 0 )

На промежутке ( -2 ; -1 ) график функции у = 0 выше у = х - 3 , следовательно при нахождении площади - из первой функции отнимем вторую.

$\displaystyle \int\limits^{-1}_{-2} {0-(x-3)} \, dx =\int\limits {- x+3} \,dx =-\frac{x^2}{2} +3x\Bigg |^{-1}_{-2}=\\-\frac{(-1)^2}{2} +3\cdot (-1) -\bigg(-\frac{(-2)^2}{2} +3\cdot (-2)\bigg)=-\frac{1}{2} -3-\bigg(-2-6\bigg)=\\=-\frac{7}{2} +8=4,5(ed)^2$

2 вариант.

Фигура , которая ограниченна графиками функций , является прямоугольной трапецией . Чтобы вычислить площадь прямоугольной трапеции, воспользуемся формулой   S = 1/2(a+b)h , где а-нижнее основание , b-верхнее основание , h-высота , в нашем случае , а = 5ед , b = 4eд , h = 1ед.

$S=\frac{1}{2} (5+4)\cdot 1=\frac{9}{2} =4,5 (ed)^2$