Предмет: Алгебра,
автор: gahsisi
ПОЖАЛУЙСТА, ПОМОГИТЕ РЕШИТЬ!!!
Приложения:
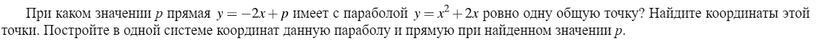
Ответы
Автор ответа:
0
Если прямая и парабола имеют одну общую точку, то эта прямая касается параболы.
Уравнение касательной к параболе:
yk = y0 + y'(x0)(x - x0).
Найдем производную:
y' = (x^2+2·x)' = 2·x+2
Свойство производной – она равна тангенсу угла наклона касательной к графику функции, по заданию – это (-2).
Приравняем: 2х + 2 = -2,
2х = -4,
x = -4/2 = -2.
y = 2^2 + 2*(-2) = 0.
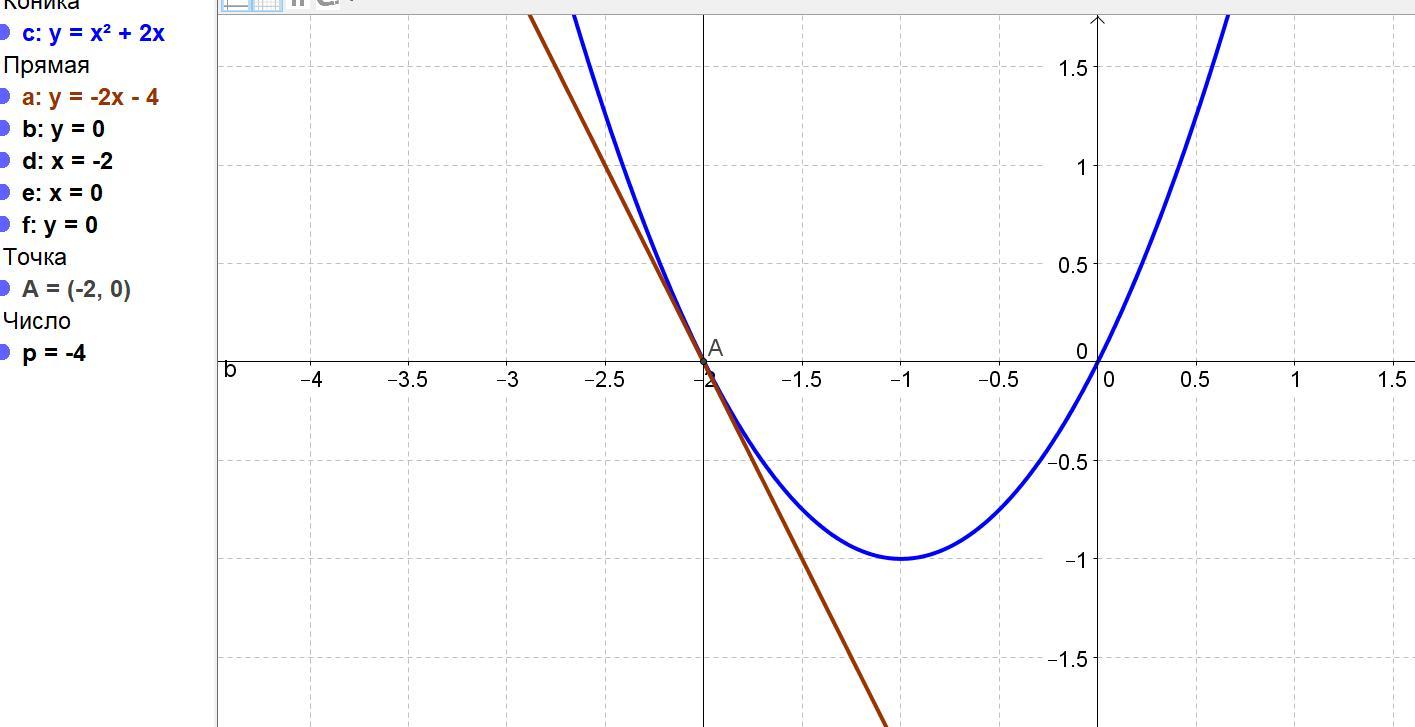
Координаты точки касания (-2; 0).
Отсюда находим значение р = у + 2х = 0 + 2*(-2) = -4.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: bezpalkoanuta
Предмет: Математика,
автор: aldiarkusniden3
Предмет: Другие предметы,
автор: erulansapabek
Предмет: География,
автор: Аноним
Предмет: Математика,
автор: EgOr133735