Question

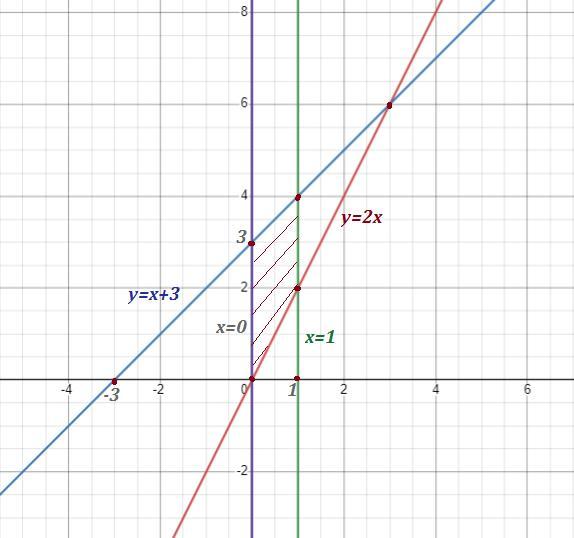
найдите объем тела полученного при вращении вокруг оси абцисс фигуры, ограниченной линиями

y=2x, y=x+3, x=0, x=1

Answer 1

Ответ:

Объяснение:

на фото

Answer 2

Ответ:

Объём тела, образованного вращением криволинейной трапеции вокруг оси ОХ , вычисляем с помощью определённого интеграла            $\bf \displaystyle V_{ox}=\pi \int\limits^{a}_{b}\, f^2(x)\, dx$   .  

В условии задана область, которая может быть представлена как разность двух криволинейных трапеций:

 $y=2x\ ,\ y=x+3\ ,\ x=0\ ,\ x=1$  

$\displaystyle V_{ox}=\pi \int\limits _0^1\Big((x+3)^2-(2x)^2\Big)\, dx=\pi \cdot \Big(\frac{(x+3)^3}{3}-\frac{4x^3}{3}\Big)\Big|_0^1=\\\\\\=\pi \cdot \Big(\frac{4^3}{3}-\frac{3^3}{3}-\frac{4}{3}\Big)=\pi \cdot \frac{64-27-4}{3}=\pi \cdot \frac{33}{3}=11\pi$  

Ответ:  $V_{ox}=11\pi$  (ед.³)