Предмет: Геометрия,
автор: Вилка96
ABCD — ромб. А = 60°, АВ = m, BE перпендикулярно ABC. Найдите угол между плоскостями AED и ABC. BE = что на картинке
Приложения:
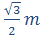
Ответы
Автор ответа:
0
опусти высоту из точки В на AD, соедини точки Е и К. получим прямоуг. треуг. ЕВК.
ВЕ перпенд. ВК, ВК перпенд. AD по т. про три перпендикуляра ЕК перпенд. AD и угол ЕКВ искомый угол( по определению угла между двумя плоскостями).BK найдем из треуг.АВК ВК=m*sin60=m*sqrt(3)/2 Получили, что в треуг.ЕВК, ВК=ВЕ, значит треуг. ЕВК равнобедр., и тогда угол ЕКВ=45 гр.
Похожие вопросы
Предмет: История,
автор: mariamaskerova
Предмет: История,
автор: Аноним
Предмет: Химия,
автор: Denysir
Предмет: Математика,
автор: vika34
Предмет: История,
автор: hirayuchiki