Question

Задание на картинке.​

Answer 1

Ответ:

Задание выполнено качественно.

Объяснение:

Удачи!

Answer 2

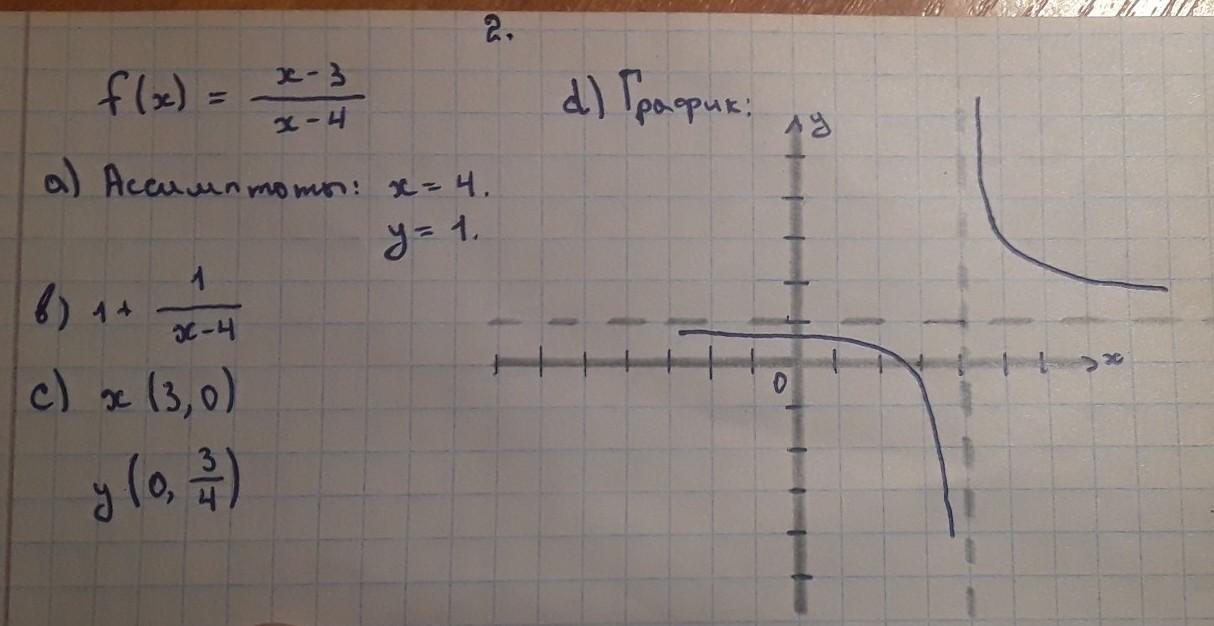
Ответ:

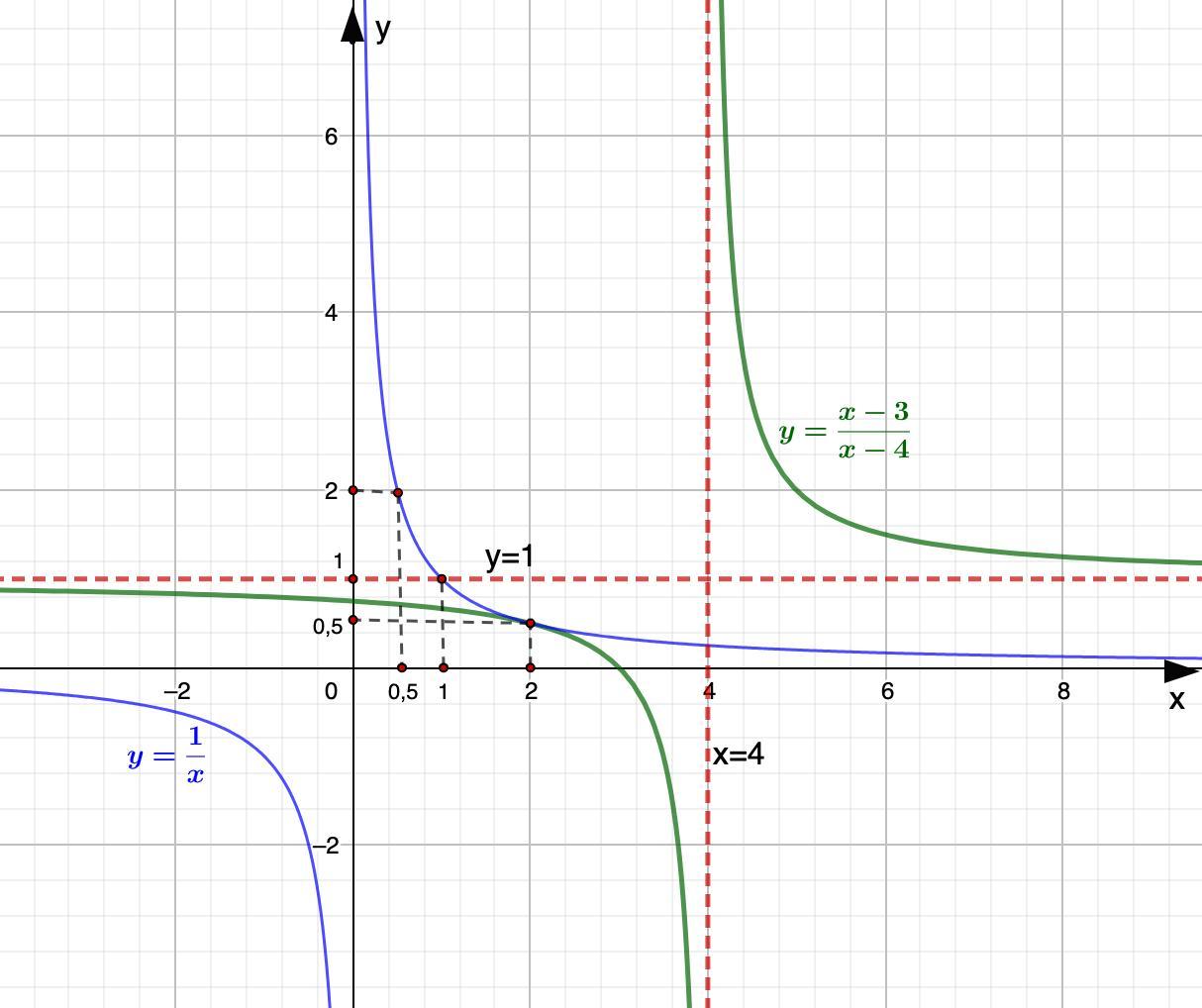
а) х = 4 - вертикальная асимптота.

у = 1 - горизонтальная асимптота.

b)  $\displaystyle \bf f(x)=1+\frac{1}{x-4}$

c)  (0; 3/4);  (3; 0)

d) см. рис.

Объяснение:

Дробно-линейная функция задана уравнением: $\displaystyle \bf f(x)=\frac{x-3}{x-4}$.

а) Найдите асимптоты функции;

в) приведите функцию  $\displaystyle \bf f(x)=\frac{x-3}{x-4}$  к виду  $\displaystyle \bf f(x)=n+\frac{k}{x+m}$;

с) найдите точки пересечения функции с осями координат;

d) постройте график функции.

                 

а) Рассмотрим данную функцию.

Знаменатель не может быть равен нулю.

⇒ х - 4 ≠ 0 или х ≠ 4.

Значит х = 4 - вертикальная асимптота.

b) Теперь приведем функцию к виду  $\displaystyle \bf f(x)=n+\frac{k}{x+m}$ и определим горизонтальную асимптоту.

$\displaystyle \bf f(x)=\frac{x-3}{x-4}=\frac{(x-4)+1}{x-4} =1+\frac{1}{x-4}$

Если х → ∞, то  $\displaystyle \bf \frac{1}{x-4}$  → 0, а f(x) → 1.

То есть у = 1 - горизонтальная асимптота.

c) Если график пересекает ось Оу, то х = 0:

$\displaystyle \bf f(0)=\frac{0-3}{0-4}=\frac{3}{4}$  ⇒ (0; 3/4)

если пересекает ось Ох, то у = 0:

$\displaystyle \bf 0=\frac{x-3}{x-4}\;\;\;\Rightarrow \;\;\;x=3$   ⇒ (3; 0)

d) Чтобы построить данный график, построим сначала график

$\displaystyle \bf y=\frac{1}{x}$  

- функция обратной пропорциональности, график - гипербола.

Дополнительные точки:

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c|c| }\cline{1-4}x& 1 & 0,5 & 2 \\\cline{1-4}y& 1 & 2 & 0,5 \\\cline{1-4}\end{array}$

Строим ветвь гиперболы. Вторая ветвь будет симметрична относительно начала координат.

График  $\displaystyle \bf f(x)=1+\frac{1}{x-4}$ получим из построенного графика путем сдвига на 4 единицы вправо и 1 единицу вверх.