Question

помогите пожалуйста с алгеброй
36 подробно ​

Answer 1

№36

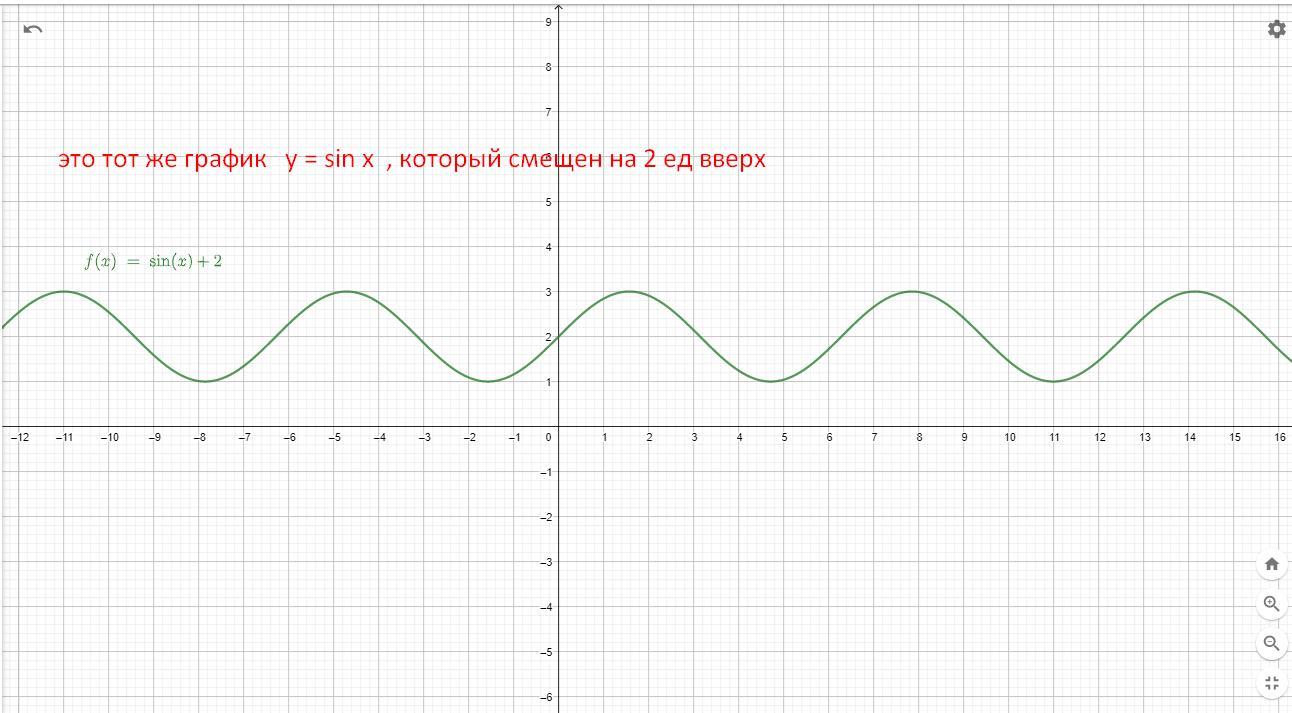
a)  y = 2 + sin x

Область определения  $x \in \mathbb R$

Чтобы найти область  значений ,      будем смотреть на область значений для функции  y = sin x  ,     $y\in [ - 1 ; 1]$

При  sinx =  - 1 , наша функция будет достигать минимума

$y_{min} = 2 - 1 = 1$

При  sinx = 1 ,  наша функция будет принимать наибольшее значение

$y _{max}= 2 + 1 = 3$

Следовательно область значений функции  y = 2 + sin x

находится на промежутке  y [ 1 ; 3]

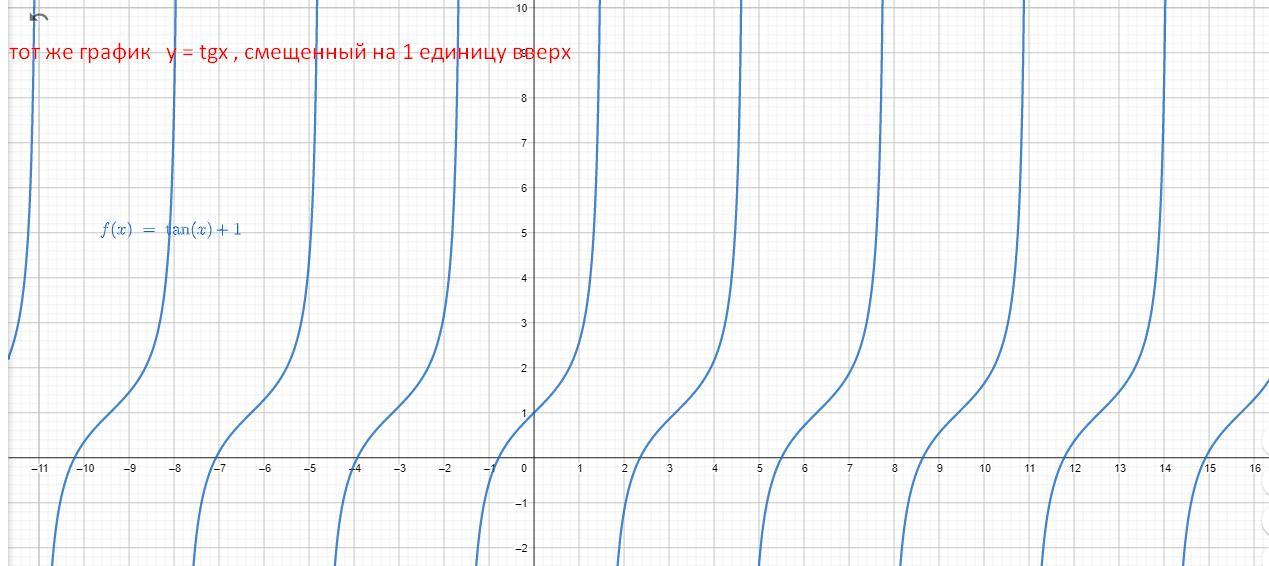
б)  y = tgx +  1

Область определения :

$x \neq \dfrac{\pi }{2} +\pi n ~ , ~ n \in \mathbb Z$

Чтобы найти область значений , также  рассмотрим  функцию  y = tgx

ее областью значений является любое действительное  число

$y \in \mathbb R$

Соответственно прибавив  1 , ее область значений никак не изменится  

Следовательно область значений функции  y = tgx + 1   является любое действительное число

 $y \in \mathbb R$

в)   y = cosx - 1

Область определения  $x \in \mathbb R$

Аналогично  находим область значений , как и в варианте  a)

y = cosx  ,   $y\in [ - 1 ; 1]$

При   cosx = -1

$y_{min} = -1 - 1 = -2$

При  cosx = 1

$y _{max} = 1 - 1= 0$

Область значений :

$y\in [ - 2 ~; ~0]$

г)  y = 3 + sinx

Область определения  $x \in \mathbb R$

Находим область значений

y = sinx  ,   $y\in [ - 1 ; 1]$

При   sinx = -1

$y_{min} = 3 - 1 = 2$

При  sinx = 1

$y _{max} = 3 + 1= 4$

Область значений :

$y\in [ 2 ~; ~4]$