Question

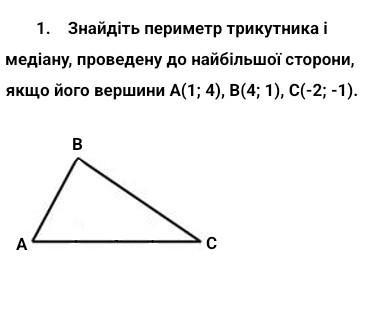
1. фото. (провести медіану)

2. Доведіть , що чотирикутник з вершинами А ( 2 ; 6 ) , B ( 5 ; 1 ) , C ( 2 ; -4 ) , D ( -1 ; 1 ) - ромб.

ПЖ ОЧЕНЬ СРОЧНО!!!​

Answer 1

Ответ:

Объяснение:

1. На графіку трикутника визначаємо найбільшу сторону - це

BС

середину ВС т . М=((Вх+Сх)/2; (Ву+Су)/2)=((4-2)/2;(1-1)/2)=(1;0)

Медіана АМ має  довжину 4

Р=|АВ|+|ВС|+|АС|

Модулі  |АВ|=√(3²+3²)=3√2=4,2 проекції векторів на осі коордінат вибрані на графіку

|ВС|=√(6²+2²)=2√10=12,6

|АС|=√(3²+5²)=11,7

Р=4,2+12,6+11,7=28,5

2. Ромб має рівні сторони ⇒

АВ=ВС=СД=АД

АВ(3;-5)

ВС(-3;-5)

СД(-3;5)

АД(-3;-5)

|АВ|=√(3²+(-5)²)=10,8

ЯК ВИДНО ИЗ КООРДІНАТ ВЕКТОРІВ квадрати їх однакові ⇒

сторони однакові  

Це ромб