Question

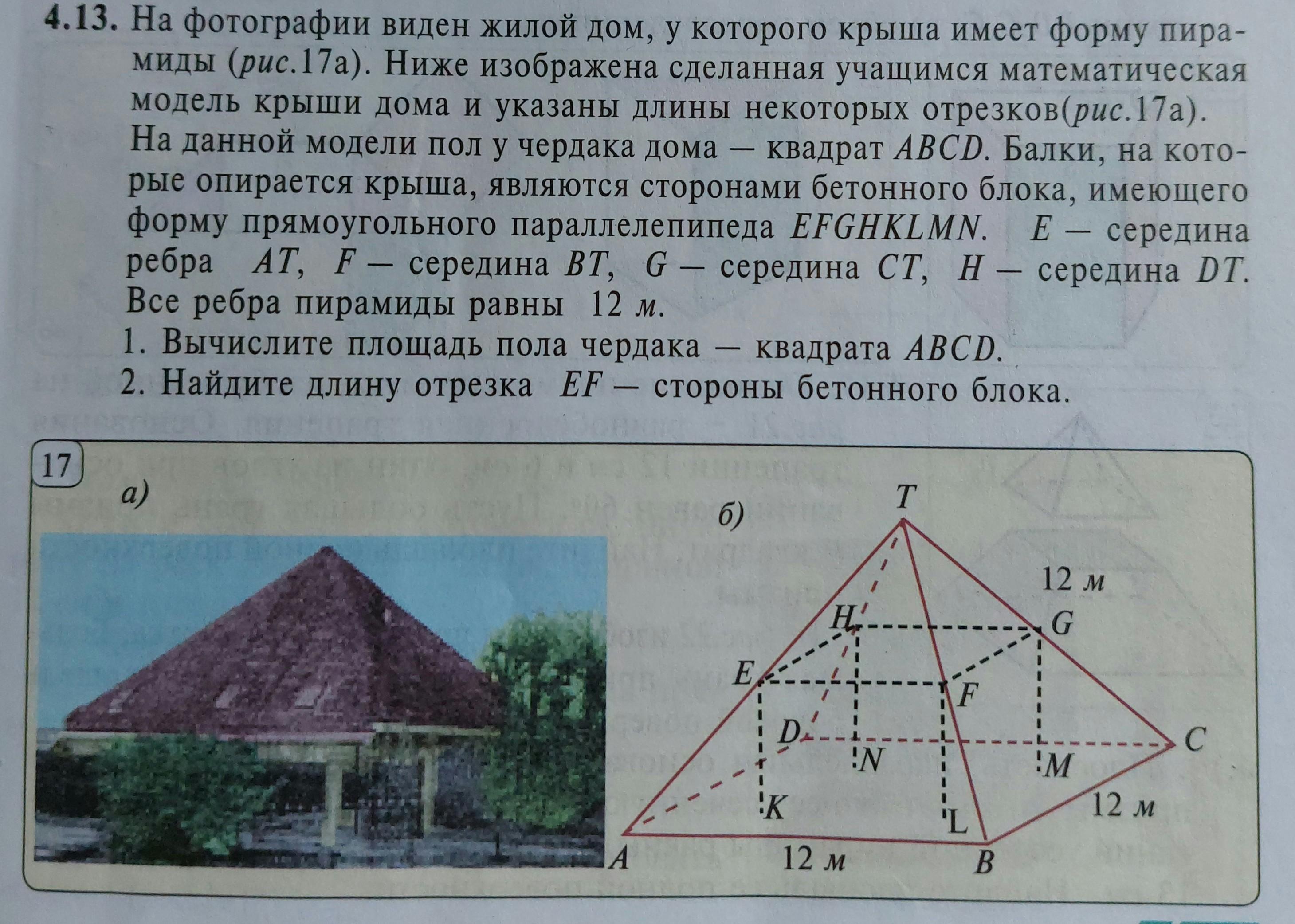
4.13. На фотографии виден жилой дом, у которого крыша имеет форму пира- миды (рис.17а). Ниже изображена сделанная учащимся математическая модель крыши дома и указаны длины некоторых отрезков(рис.17а). На данной модели пол у чердака дома квадрат ABCD. Балки, на кото- рые опирается крыша, являются сторонами бетонного блока, имеющего форму прямоугольного параллелепипеда EFGHKLMN. E - середина ребра AT, F - середина BT, G - середина CT, H - середина DT. Все ребра пирамиды равны 12 м.
1)Вычислите площадь пола чердака- квадрата ABCD
2) Найдите длину отрезка EF-- стороны бетонного блока

Answer 1

Ответ:

288√2м³

Объяснение:

ABCD- квадрат

АС=АВ√2=12√2м диагональ квадрата

АО=АС/2=12√2/2=6√2м .

∆SAO- прямоугольный треугольник

По теореме Пифагора

SO=√(SA²-AO²)=√(12²-(6√2)²)=√(144-72)=

√72=6√2м высота пирамиды.

Sосн=АВ²=12²=144м²

V=1/3*Sосн*SO=1/3*144*6√2=288√2м³