Предмет: Алгебра,
автор: alenakuznewova92
Vx = 4.10. Известно, что f(x) = x; g(x) = √x, q(x) = x²-3. Составьте сложную функцию f(g(ф(x))) и найдите ее область определения.
Приложения:
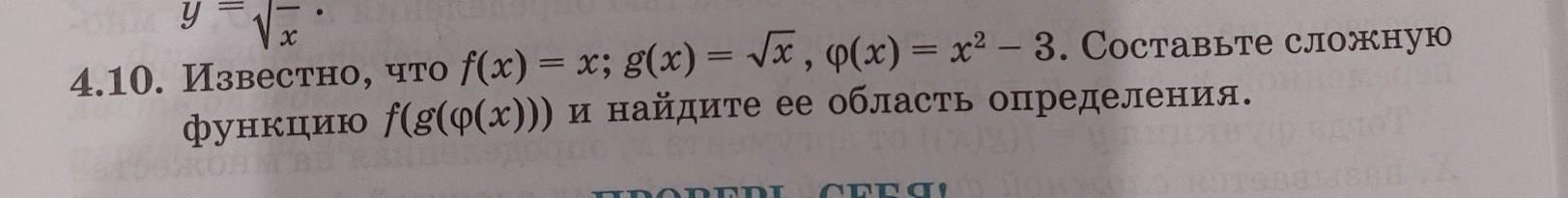
Ответы
Автор ответа:
2
Составим требуемую сложную функцию:
Найдем область определения полученной функции. Так как подкоренное выражение должно быть неотрицательным, то:
Ответ:
Похожие вопросы
Предмет: Алгебра,
автор: ponatnopon99993
Предмет: Математика,
автор: cadme067
Предмет: Қазақ тiлi,
автор: baizhanovaa09
Предмет: Музыка,
автор: tchiraeva